练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若x，y为实数，且满足|x-3|+
    		y+3
    =0    ，则(
    x
    y
    )2013    的值是
    -1
    -1
    ．
    分析：根据非负数的性质列式求出x、y的值，然后代入代数式进行计算即可得解．
    解答：解：根据题意得，x-3=0，y+3=0，
    解得x=3，y=-3，
    所以，（
    x
    y
    ）2013=（
    3
    -3
    ）2013=-1．
    故答案为：-1．
    点评：本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，抛物线y=a（x+1）（x-5）与x轴的交点为M，N．直线y=kx+b与x轴交于P（-2，0），与y轴交于C．若A，B两点在直线y=kx+b上，且AO=BO=
    		2
    ，AO⊥BO．D为线段MN的中点，OH为Rt△OPC斜边上的高．
    （1）OH的长度等于
     
    ；k=
     
    ，b=
     
    ；
    （2）是否存在实数a，使得抛物线y=a（x+1）（x-5）上有一点E，满足以D，N，E为顶点的三角形与△AOB相似？若不存在，说明理由；若存在，求所有符合条件的抛物线的解析式，同时探索所求得的抛物线上是否还有符合条件的E点（简要说明理由）；并进一步探索对符合条件的每一个精英家教网E点，直线NE与直线AB的交点G是否总满足PB•PG＜10
    		2
    ，写出探索过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

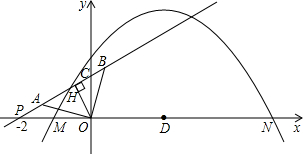
    如图，抛物线y＝a(x＋1)(x－5)与x轴的交点为M、N．直线y＝kx＋b

    与x轴交于P(－2，0)，与y轴交于C．若A、B两点在直线y＝kx＋b上，且AO=BO=，AO⊥BO．D为线段MN的中点，OH为Rt△OPC斜边上的高．

    1.OH的长度等于___________；k＝___________，b＝____________；

    2.是否存在实数a，使得抛物线y＝a(x＋1)(x－5)上有一点E，满足以D、N、E为顶点的三角形与△AOB相似?若不存在，说明理由；若存在，求所有符合条件的抛物线的解析式，同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由)；并进一步探索对符合条件的每一个E点，直线NE与直线AB的交点G是否总满足PB·PG＜，写出探索过程．

     

     

     

     

     

     

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （本题满分12分）如图，抛物线y＝a(x＋1)(x－5)与x轴的交点为M、N．直线y＝kx＋b

    与x轴交于P(－2，0)，与y轴交于C．若A、B两点在直线y＝kx＋b上，且AO=BO=，AO⊥BO．D为线段MN的中点，OH为Rt△OPC斜边上的高．

    (1)OH的长度等于___________；k＝___________，b＝____________；

    (2)是否存在实数a，使得抛物线y＝a(x＋1)(x－5)上有一点E，满足以D、N、E为顶

    点的三角形与△AOB相似?若不存在，说明理由；若存在，求所有符合条件的抛物线的解析式，同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由)；并进一步探索对符合条件的每一个E点，直线NE与直线AB的交点G是否总满足PB·PG＜，写出探索过程．

     

    查看答案和解析>>

    科目：初中数学 来源：第27章《二次函数》中考题集（36）：27.3 实践与探索（解析版） 题型：解答题

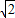    如图，抛物线y=a（x+1）（x-5）与x轴的交点为M，N．直线y=kx+b与x轴交于P（-2，0），与y轴交于C．若A，B两点在直线y=kx+b上，且AO=BO=，AO⊥BO．D为线段MN的中点，OH为Rt△OPC斜边上的高．
    （1）OH的长度等于______；k=______，b=______；
    （2）是否存在实数a，使得抛物线y=a（x+1）（x-5）上有一点E，满足以D，N，E为顶点的三角形与△AOB相似？若不存在，说明理由；若存在，求所有符合条件的抛物线的解析式，同时探索所求得的抛物线上是否还有符合条件的E点（简要说明理由）；并进一步探索对符合条件的每一个E点，直线NE与直线AB的交点G是否总满足PB•PG＜10，写出探索过程．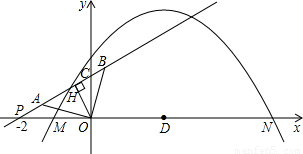

    查看答案和解析>>

    科目：初中数学 来源：第2章《二次函数》中考题集（35）：2.4 二次函数的应用（解析版） 题型：解答题

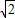    如图，抛物线y=a（x+1）（x-5）与x轴的交点为M，N．直线y=kx+b与x轴交于P（-2，0），与y轴交于C．若A，B两点在直线y=kx+b上，且AO=BO=，AO⊥BO．D为线段MN的中点，OH为Rt△OPC斜边上的高．
    （1）OH的长度等于______；k=______，b=______；
    （2）是否存在实数a，使得抛物线y=a（x+1）（x-5）上有一点E，满足以D，N，E为顶点的三角形与△AOB相似？若不存在，说明理由；若存在，求所有符合条件的抛物线的解析式，同时探索所求得的抛物线上是否还有符合条件的E点（简要说明理由）；并进一步探索对符合条件的每一个E点，直线NE与直线AB的交点G是否总满足PB•PG＜10，写出探索过程．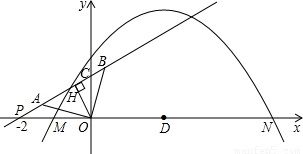

    查看答案和解析>>

    同步练习册答案