
分析 (1)把x=0代入,可得到关于c的方程,可求得c的值;
(2)把x=3代入可得到关于a、b的关系式,结合c=-1,可求得答案;
(3)由(2)的关系式结合条件可求得a+b的符号,结合c=-1可比较其大小.
解答 解(1)把x=0代入代数式,得到ax5+bx3+3x+c=c=-1;
∴c=-1;
(2)把x=3代入代数式,得到ax5+bx3+3x+c=35a+33b+3×3+c=9,
∴35a+33b+c=0;35a+33b=-c=1,
当x=-3时,
原式=(-3)5a+(-3)3b+3×(-3)+c
=-(35a+33b)-9+c
=c-9+c=2c-9
=-2-9
=-11;
(3)由(2)题得35a+33b=1,即9a+b=$\frac{1}{27}$,
又∵3a=5b,所以15b+b=$\frac{1}{27}$,
∴b=$\frac{1}{432}$>0,
则a=$\frac{5}{3}$b>0,
∴a+b>0,
∵c=-1<0,
∴a+b>c.
点评 本题主要考查求代数式的值,注意整体思想的运用.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
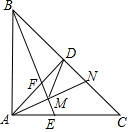 如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM.下列结论:①AE=AF;②AM⊥EF;③AF=DF;④DF=DN,其中正确的结论有( )
如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM.下列结论:①AE=AF;②AM⊥EF;③AF=DF;④DF=DN,其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
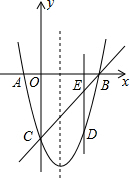 如图,抛物线y=x2-4x-5与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E.
如图,抛物线y=x2-4x-5与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com