
【题目】用适当的方法解下列方程:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() ;(5)5x(x-3)=6-2x;(6)3y2+1=
;(5)5x(x-3)=6-2x;(6)3y2+1= ![]() .
.
【答案】(1)![]() (2)1或0;(3)4或-
(2)1或0;(3)4或-![]() ;(4 )10或-12;(5)3或
;(4 )10或-12;(5)3或![]() ;(6)
;(6) ![]() .
.
【解析】试题分析:(1)用一元二次方程的求根公式求出方程的根;
(2)把右边的项移到左边,用提公因式法因式分解求出方程的根;
(3)把右边的项移到左边用平方差公式因式分解求出方程的根;
(4)把常数项移到右边,用直接开平方法求出方程的根.
(5)首先对方程的右边提取公因式-3,然后移项,提取公因式x-3后即可求解;
(6)将3y2转化为(![]() y)2后即可利用完全平方公式因式分解.
y)2后即可利用完全平方公式因式分解.
试题解析:(1)x26x3=0,
a=1,b=6,c=3,
△=36+12=48,
x=![]() =
=![]() =3±
=3±![]() ,
,
∴x1=3+![]() ,x2=3
,x2=3![]() ;
;
(2)x(x+1)2x=0,
x(x+12)=0,
x=0或x1=0,
∴x1=0,x2=1;
(3)(x+3)2(12x)2=0,
(x+3+12x)(x+31+2x)=0,
(4x)(3x+2)=0,
4x=0或3x+2=0,
∴x1=4,x2=![]() ;
;
(4)x2+2x=120,
x2+2x+1=121,
(x+1)2=121,
x+1=±11,
∴x1=10,x2=12.
(5)5x(x3)=62x
方程变形为:5x(x3)=3(x3)
移项得:(x3)(5x+3)=0;
解得:x1=3,x2=![]() ;
;
(6)3y2+1=![]() y.
y.
方程变形为:(![]() y)22
y)22![]() y+1=0,
y+1=0,
即:(![]() y1)2=0
y1)2=0
解得:x1=x2=![]() .
.


科目:初中数学 来源: 题型:
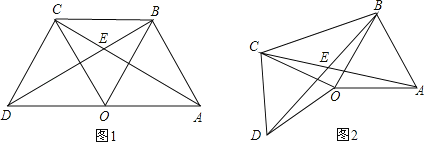
【题目】(1)如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小;
(2)如图2,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕点O旋转(△OAB和△OCD不能重叠),求∠AEB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作AC的垂直平分线,交AB于点O,交AC于点D;
②以O为圆心,OA为半径作圆,交OD的延长线于点E.
(2)在(1)所作的图形中,解答下列问题.
①点B与⊙O的位置关系是__;(直接写出答案)
②若DE=2,AC=8,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公路AB和公路CD在点P处交会,且∠APC=45°,点Q处有一所小学,PQ=![]() ,假设拖拉机行驶时,周围130m以内会受到噪声的影响,那么拖拉机在公路AB上沿PA方向行驶时,学校是否会受到噪声影响?请说明理由;若受影响,已知拖拉机的速度为36km/h,那么学校受影响的时间为多少秒?
,假设拖拉机行驶时,周围130m以内会受到噪声的影响,那么拖拉机在公路AB上沿PA方向行驶时,学校是否会受到噪声影响?请说明理由;若受影响,已知拖拉机的速度为36km/h,那么学校受影响的时间为多少秒?

查看答案和解析>>
科目:初中数学 来源: 题型:
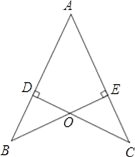
【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
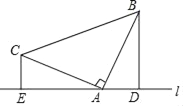
【题目】已知:如图所示,△ABC中,∠BAC=90°,AB=AC,分别过点B、C作经过点A的直线l的垂线段BD、CE,垂足分别D、E.
(1)求证:DE=BD+CE.
(2)如果过点A的直线经过∠BAC的内部,那么上述结论还成立吗?请画出图形,直接给出你的结论(不用证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.

(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点C距守门员多少米?(取![]() )
)
(3)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000000037毫克可用科学记数法表示为( )
A.3.7×10﹣5克
B.3.7×10﹣6克
C.37×10﹣7克
D.3.7×10﹣8克
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com