
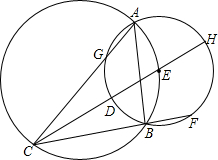
 如图,⊙E的圆心在⊙O上,⊙E交⊙O于A、B两点,⊙O的弦CE所在直线交⊙E于点D、H,CB的延长线交⊙E于点F.
如图,⊙E的圆心在⊙O上,⊙E交⊙O于A、B两点,⊙O的弦CE所在直线交⊙E于点D、H,CB的延长线交⊙E于点F.分析 (1)作EM⊥AG于M,EN⊥BF与N,连结EA、EB、AD、EF,EG,如图,利用垂径定理得到AM=MG,BN=FN,先利用圆周角定理得到∠ACE=∠BCE,再根据角平分线性质得EM=EN,接着证明Rt△AEM≌Rt△FEN得到AM=FN,∠EAM=∠EFC,然后证明∠DAG=∠DAB得到AD平分∠BAC,于是根据内心的定义即可得到结论;
(2)由(1)AG=BF进行计算即可.
解答 (1)证明:作EM⊥AG于M,EN⊥BF与N,连结EA、EB、AD、EF,EG,如图,则AM=MG,BN=FN,
∵EA=EB,
∴$\widehat{AE}$=$\widehat{BE}$,
∴∠ACE=∠BCE,
∴EM=EN,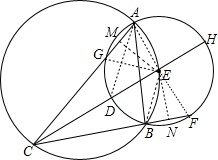
在Rt△AEM和Rt△FEN中
$\left\{\begin{array}{l}{EA=EF}\\{EM=EN}\end{array}\right.$
∴Rt△AEM≌Rt△FEN,
∴AM=FN,∠EAM=∠EFC,
∴AG=BF,
∴∠AEG=∠FEB,
∵∠ACE=∠FCE,∠CAE=∠CFE,
∴∠CEA=∠CEF,
∴∠CEG=∠CEB,
∴∠DAG=∠DAB,
∴AD平分∠BAC,
∵CD平分∠ACB,
∴点D是△ABC的内心;
(2)由(1)得AG=BF,
∴$\frac{AG}{BF}$=1.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了圆周角定理、角平分线的性质和三角形全等的判定与性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于G.
已知,如图,四边形ABCD是平行四边形,E是AB延长线上一点,DE交对角线AC于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题.
某数学兴趣小组的同学再一次探究中发现:若平面直角坐标系中有两点A(x1,y1)和B(x2,y2),则线段AB的中点C的坐标为($\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2}$).经过进一步的讨论,他们呢借助中位线和一次函数的知识证明了这一结论,请你使用该结论解答下面问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com