
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
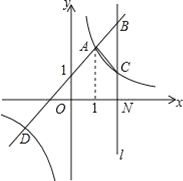
【答案】(1)反比例函数的解析式为:y=![]() ,一次函数的解析式为:y=x+1;(2)当﹣2<x<0或x>1时,一次函数的值大于反比例函数的值;(3)S△ABC=
,一次函数的解析式为:y=x+1;(2)当﹣2<x<0或x>1时,一次函数的值大于反比例函数的值;(3)S△ABC=![]() .
.
【解析】试题分析:(1)由反比例函数经过点D(﹣2,﹣1),即可求得反比例函数的解析式;然后求得点A的坐标,再利用待定系数法求得一次函数的解析式;
(2)结合图象求解即可求得x在什么范围内,一次函数的值大于反比例函数的值;
(3)首先过点A作AE⊥x轴交x轴于点E,由直线l与x轴垂直于点N(3,0),可求得点E,B,C的坐标,继而求得答案.
试题解析:(1)∵反比例函数经过点D(﹣2,﹣1),
∴把点D代入y=![]() (m≠0),
(m≠0),
∴﹣1=![]() ,∴m=2,∴反比例函数的解析式为:y=
,∴m=2,∴反比例函数的解析式为:y=![]() ,
,
∵点A(1,a)在反比例函数上,∴把A代入y=![]() ,得到a=
,得到a=![]() =2,∴A(1,2),
=2,∴A(1,2),
∵一次函数经过A(1,2)、D(﹣2,﹣1),
∴把A、D代入y=kx+b (k≠0),得到: ![]() ,解得:
,解得: ![]() ,
,
∴一次函数的解析式为:y=x+1;
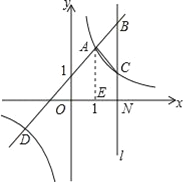
(2)如图:当﹣2<x<0或x>1时,一次函数的值大于反比例函数的值;
(3)过点A作AE⊥x轴交x轴于点E,
∵直线l⊥x轴,N(3,0),∴设B(3,p),C(3,q),
∵点B在一次函数上,∴p=3+1=4,
∵点C在反比例函数上,∴q=![]() ,
,
∴S△ABC=![]() BCEN=
BCEN=![]() ×(4﹣
×(4﹣![]() )×(3﹣1)=
)×(3﹣1)=![]() .
.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】有一天,龟、兔进行了600米赛跑,如图表示龟兔赛跑的路程s(米)与时间t(分钟)的关系(兔子睡觉前后速度保持不变),根据图象回答以下问题:
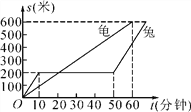
(1)赛跑中,兔子共睡了多少时间?
(2)赛跑开始后,乌龟在第几分钟时从睡觉的兔子旁经过?
(3)兔子跑到终点时,乌龟已经到了多长时间?并求兔子赛跑的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年4月14日日本熊本县发生6.2级地震,据NHK报道,受强地震造成的田地受损,农产品无法出售等影响,日本熊本县农林业遭受的地震损失最少可达236亿日元,数据236亿用科学记数法表示为( )
A.2.36×108
B.2.36×109
C.2.36×1010
D.2.36×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在选拔2016年第十三届全国冬季运动会速滑运动员时,教练打算根据平时训练成绩,从运动员甲和乙种挑选1名成绩稳定的运动员,甲、乙两名运动员平时训练成绩的方差分别为S甲2=0.03,S乙2=0.20,你认为教练应该挑选的运动员是( )
A.乙
B.甲
C.甲、乙都行
D.无法判断
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2﹣(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.
(1)求m的值;
(2)求A、B两点的坐标;
(3)当﹣3<x<1时,在抛物线上是否存在一点P,使得△PAB的面积是△ABC面积的2倍?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=![]() (x>0)的图象上,点D的坐标为(4,3).
(x>0)的图象上,点D的坐标为(4,3).
(1)求k的值;
(2)将这个菱形沿x轴正方向平移,当顶点D落在反比例函数图象上时,求菱形平移的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核,三人各项得分如表:
笔试 | 面试 | 体能 | |
甲 | 84 | 78 | 90 |
乙 | 85 | 80 | 75 |
丙 | 80 | 90 | 73 |
![]() 根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
![]() 该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按
该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按![]() 的比例计入总分
的比例计入总分![]() 根据规定,请你说明谁将被录用.
根据规定,请你说明谁将被录用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com