
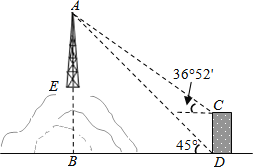
【题目】如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
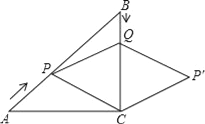
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,若四边形QPCP′为菱形,则t的值为_____.
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,若四边形QPCP′为菱形,则t的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,动点P从直角梯形ABCD的直角顶点B出发,沿BCDA的顺序运动,得到以点P移动的路程x为自变量,△ABP面积y为函数的图象,如图2,则梯形ABCD的面积是( )
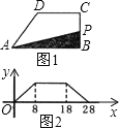
A. 104B. 120C. 80D. 112
查看答案和解析>>
科目:初中数学 来源: 题型:
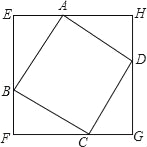
【题目】如图,正方形ABCD的四个顶点分别在正方形EFGH的四条边上,我们称正方形EFGH是正方形ABCD的外接正方形.
探究一:巳知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的2倍?如图,假设存在正方形EFGH,它的面积是正方形ABCD的2倍.
因为正方形ABCD的面积为1,则正方形EFGH的面积为2,
所以EF=FG=GH=HE=![]() ,设EB=x,则BF=
,设EB=x,则BF=![]() ﹣x,
﹣x,
∵Rt△AEB≌Rt△BFC
∴BF=AE=![]() ﹣x
﹣x
在Rt△AEB中,由勾股定理,得
x2+(![]() ﹣x)2=12
﹣x)2=12
解得,x1=x2=![]()
∴BE=BF,即点B是EF的中点.
同理,点C,D,A分别是FG,GH,HE的中点.
所以,存在一个外接正方形EFGH,它的面积是正方形ABCD面积的2倍
探究二:巳知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的3倍?(仿照上述方法,完成探究过程)
探究三:巳知边长为1的正方形ABCD, 一个外接正方形EFGH,它的面积是正方形ABCD面积的4倍?(填“存在”或“不存在”)
探究四:巳知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的n倍?(n>2)(仿照上述方法,完成探究过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“朗读者”节目的影响下,某中学开展了“好书伴我成长”的读书活动,为了解3月份七年级300名学生读书情况,随机调查了七年级50个学生读书的册数,统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 4 | 12 | 16 | 17 | 1 |
关于这组数据,下列说法正确的是( )
A. 众数是 17 B. 平均数是 2 C. 中位数是 2 D. 方差是 2
查看答案和解析>>
科目:初中数学 来源: 题型:
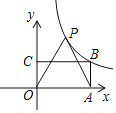
【题目】如图,矩形OABC的顶点A,C分别在x轴,y轴上,顶点B在第一象限,AB=1.将线段OA绕点O按逆时针方向旋转60°得到线段OP,连接AP,反比例函数![]() (k≠0)的图象经过P,B两点,则k的值为______________.
(k≠0)的图象经过P,B两点,则k的值为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
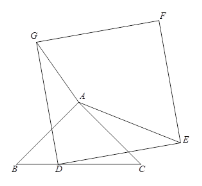
【题目】如图,已知△ABC中,∠BAC=90°,AB=AC=6.D为BC边一点,且BD∶DC=1∶2,以D为一个顶点作正方形DEFG,且DE=BC,连接AE,将正方形DEFG绕点D旋转一周,在整个旋转过程中,当AE取得最大值时AG的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求![]() 的值.
的值.
(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的![]() 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
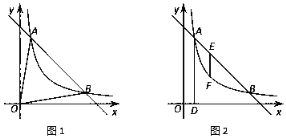
【题目】如图1,点A(m,6),B(6,1)在反比例函数图象上,作直线AB,连接OA、OB.
(1)求反比例函数的表达式和m的值;
(2)求△AOB的面积;
(3)如图2,E是线段AB上一点,作AD⊥x轴于点D,过点E作x轴的垂线,交反比例函数图象于点F,若EF=![]() AD,求出点E的坐标.
AD,求出点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com