
����Ŀ�������dz�����ѧ��һ����Ҫ���ߣ�����������Խ������������ؽ�ϣ��о��������Ƿ��֣��������ϵ�A����B��ʾ�����ֱ�Ϊa��b����A��B����֮��ľ���AB��|a��b|���߶�AB���е��ʾ����Ϊ![]() ���磺��ͼ�������ϵ�A��ʾ����Ϊ��2����B��ʾ����Ϊ8����A�������ľ���AB��|��2��8|��10���߶�AB���е�C��ʾ����Ϊ
���磺��ͼ�������ϵ�A��ʾ����Ϊ��2����B��ʾ����Ϊ8����A�������ľ���AB��|��2��8|��10���߶�AB���е�C��ʾ����Ϊ![]() ��3����P�ӵ�A��������ÿ��3����λ���ȵ��ٶ����������������˶���ͬʱ��Q�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������˶������˶�ʱ��Ϊt�루t��0����
��3����P�ӵ�A��������ÿ��3����λ���ȵ��ٶ����������������˶���ͬʱ��Q�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������˶������˶�ʱ��Ϊt�루t��0����
��1���ú�t�Ĵ���ʽ��ʾ��t���P��ʾ����Ϊ�� ������Q��ʾ����Ϊ�� ����
��2����tΪ��ֵʱ��P��Q������������д������������ʾ������
��3����tΪ��ֵʱ��PQ��![]() AB��
AB��
��4������MΪPA���е㣬��NΪPB���е㣬��P���˶������У��߶�MN�ij����Ƿ����仯�����仯����˵�����ɣ������䣬������߶�MN�ij���
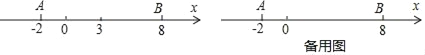
���𰸡���1��-2+3t��8-2t����2���������ʾ����Ϊ4����3����t=1��3ʱ��PQ=![]() AB����4����P���˶������У��߶�MN�ij��Ȳ������仯�����ɼ�����.
AB����4����P���˶������У��߶�MN�ij��Ȳ������仯�����ɼ�����.
��������
��1���������⣬�����ú�t�Ĵ���ʽ��ʾ����P�͵�Q��
��2�����ݵ�P��Q��������ʱ��P��Q��ʾ������ȣ����Եõ�����t�ķ��̣�Ȼ�����t��ֵ��������Խ����
��3������PQ=![]() AB�����������Ӧ��t��ֵ��
AB�����������Ӧ��t��ֵ��
��4������������Ա�ʾ����M�͵�N���Ӷ����Խ���⣮
��1��������ɵã�
t���P��ʾ����Ϊ��-2+3t����Q��ʾ����Ϊ��8-2t��
�ʴ�Ϊ��-2+3��8-2t��
��2���ߵ�P��Q��������ʱ��P��Q��ʾ������ȣ�
��-2+3t=8-2t��
��ã�t=2��
�൱t=2ʱ��P��Q������
��ʱ��-2+3t=-2+3��2=4��
���������ʾ����Ϊ4��
��3����t���P��ʾ����-2+3t����Q��ʾ����Ϊ8-2t��
��PQ=|��-2+3t��-��8-2t��|=|5t-10|��
��![]()
��|5t-10|=5��
��ã�t=1��3��
�൱t=1��3ʱ��PQ=![]() AB��
AB��
��4����P���˶������У��߶�MN�ij��Ȳ������仯��
�������£��ߵ�M��ʾ����Ϊ�� ![]()
��N��ʾ����Ϊ�� ![]()
��MN=![]()
���P���˶������У��߶�MN�ij��Ȳ������仯��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
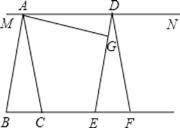
����Ŀ����ͼ��ʾ����![]() ��ֱ��BC����ƽ��
��ֱ��BC����ƽ��![]() ��λ�ã�G��DE��һ�㣬����AG������A��D��ֱ��MN��
��λ�ã�G��DE��һ�㣬����AG������A��D��ֱ��MN��
(1)��֤��![]() ��
��
(2)��![]() ��
��![]() ���ж�AG��DE��λ�ù�ϵ����֤����Ľ��ۣ�
���ж�AG��DE��λ�ù�ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
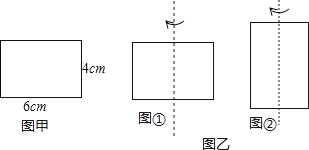
����Ŀ��̽������һ��6cm����4cm�ľ���ֽ�壬��Ҫ������һ��Ա��е�����ֱ��Ϊ�ᣬ��ת180�����õ�һ��Բ�����ֿɰ������ַ������в�����
����һ���Խϳ���һ��Ա��е�����ֱ��Ϊ����ת����ͼ�٣�
���������Խ϶̵�һ��Ա��е�����ֱ��Ϊ����ת����ͼ�ڣ�
��1����ͨ������˵�����ַ��������Բ�������
��2������þ��εij����ֱ���5cm��3cm�أ���ͨ������˵�����ַ��������Բ�������
��3��ͨ������̽�����㷢�ֶ���ͬһ�����Σ������������Σ�������һ��Ա��е�����ֱ��Ϊ����ת�õ�һ��Բ���������������õ���Բ���������˵��ԭ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AB=3��AD=4����ABC=60�㣬��BC���е�E��EF��AB������Ϊ��F����DC���ӳ����ཻ�ڵ�H�����DEF������� �� 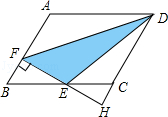
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У�E��CA�ӳ����ϵĵ㣬F��AC�ӳ����ϵĵ㣬��AE=CF����֤��
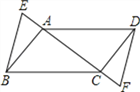
��1����ABE�ա�CDF��
��2��BE��DF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ����PΪ��O��һ�㣬��OP��BC����P=��BAC�� 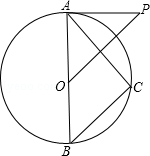
��1����֤��PAΪ��O�����ߣ�
��2����OB=5��OP= ![]() ����AC�ij���
����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��l1 �� l2�ֱ���A��1��0������B����3��0�������ҵ���ֱ��ͬʱ�ཻ��y������ĵ�Cʱ��ǡ����l1��l2 �� ������A��B��C�������ߵĶԳ�����ֱ��l1���ڵ�K����ͼ��ʾ��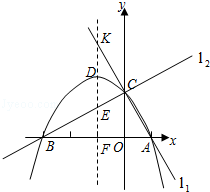
��1�����C�����꣬����������ߵĺ�������ʽ��
��2�������ߵĶԳ��ᱻֱ��l1 �� �����ߣ�ֱ��l2��x�����νص������߶Σ����������߶��к�������ϵ����˵�����ɣ�
��3����ֱ��l2�Ƶ�C��תʱ���������ߵ���һ������ΪM�����ҳ�ʹ��MCKΪ���������εĵ�M���������ɣ���д����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
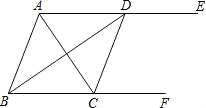
����Ŀ����ͼ��AE��BF��ACƽ�֡�BAE����BF�ڵ�C��BDƽ�֡�ABC����AE�ڵ�D������CD��
��1����֤���ı���ABCD�����Σ�
��2����AB=5��AC=6����AE��BF֮��ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. ��2��x+1��=x+7ȥ���š�����ϲ�ͬ�����x=5
B. ��![]() =1+
=1+![]() ȥ��ĸ����2��2x��1��=1+3��x��3��
ȥ��ĸ����2��2x��1��=1+3��x��3��
C. ��2��2x��1����3��x��3��=1ȥ���ţ���4x��2��3x��9=1
D. ��7x=4x��3�����7x��4x=3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com