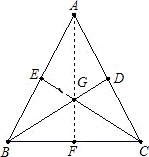
已知:BD、CE是△ABC的两条中线(如图),BD=CE
求证:AB=AC.
证明1:作中线AF,则三条中线交于重心G.
∵
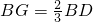
,
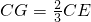
,
∴BG=CG;
∴GF⊥BC,即AF⊥BC.
又∵AF是中线,
∴AB=AC.
证明2:如图,将EC沿ED平移得DF,连接ED、CF,则四边形EDFC是平行四边形,
∴DF=EC,
而EC=BD,
∴BD=DF.
又∵D、E分别AC、AB的中点,
∴DE∥BC,
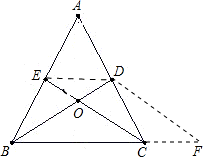
∴B、C、F三点共线.
∴∠DBF=∠DFB=∠ECB,
又∵BD=CE,BC=CB,
∴△ECB≌△DBC(SAS),
∴∠ABC=∠ACB,
∴AB=AC.
分析:此题分两种情况证明,证明1:作中线AF,则三条中线交于重心G.有重心性质可证BG=CG,再根据等腰三角形三线合一的性质即可证GF⊥BC,再利用AF是中线,即可证明结论;
证明2:如图,将EC沿ED平移得DF,连接ED、CF,则四边形EDFC是平行四边形,由BD=EC=DF.D、E分别AC、AB的中点,可证B、C、F三点共线,可得∠DBF=∠DFB=∠ECB,再利用(SAS)求证△ECB≌△DBC即可.
点评:此题主要考查等腰三角形的性质和全等三角形的判定与性质等知识点的理解和掌握,此题有两种情况,特别是证明2学生容易忽视,因此要向学生特别强调.

 已知:BD、CE是△ABC的两条中线(如图),BD=CE
已知:BD、CE是△ABC的两条中线(如图),BD=CE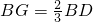 ,
,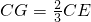 ,
,


 名校课堂系列答案
名校课堂系列答案