
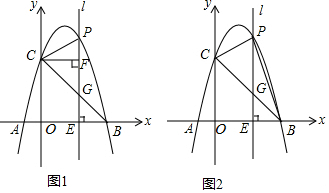
 ��ͼ����֪��ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣬��A��B�ֱ���x���ϣ���A��ԭ����࣬��B��ԭ���Ҳࣩ��OB=4OA��������A��B�������߽�y���ڵ�C��0��2�����ҡ�ACB=90�㣮
��ͼ����֪��ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣬��A��B�ֱ���x���ϣ���A��ԭ����࣬��B��ԭ���Ҳࣩ��OB=4OA��������A��B�������߽�y���ڵ�C��0��2�����ҡ�ACB=90�㣮���� ��1����ͼ1�У�������OB=4OA����OA=m����OB=4m��֪��ACO�ס�CBO���ɵ�OC2=OA•OB���Ƴ�m=1��-1���������ɵ�A��-1��0����B��4��0�����������ߵĽ���ʽΪy=a��x+1����x-4�����ѣ�0��2������õ�a=-$\frac{1}{2}$���ɽ�����⣻
��2����취���ֱ��ON�Ľ���ʽ�����÷������������N�����꼴�ɽ�����⣻
��3���������������ۣ�����ͼ2�У�����BED=90��ʱ����BED�ס�BCA������ͼ3�У�����EDB=90��ʱ����BDE�ס�BCA���ֱ���⼴�ɣ�
��� �⣺��1����ͼ1�У�������OB=4OA����OA=m����OB=4m��
�ߡ�ACB=90�㣬��֪��ACO�ס�CBO��
��ɵ�OC2=OA•OB��
��4m2=4��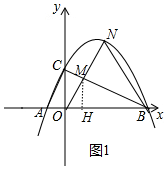
��m=1��-1��������
��A��-1��0����B��4��0����
�������ߵĽ���ʽΪy=a��x+1����x-4����
�ѣ�0��2������õ�a=-$\frac{1}{2}$��
�������ߵĽ���ʽΪy=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
��2����ͼ1�У���ON��BC��M����MH��AB��H��
�ߡ�COM=��CBO����COM=��OCB��
���OCM�ס�BCO��
��OC2=CM•CB��
��4=CM•2$\sqrt{5}$��
��CM=$\frac{2\sqrt{5}}{5}$��MB=$\frac{8\sqrt{5}}{5}$��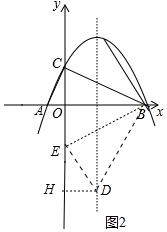
��MH��OC��
��$\frac{MH}{OC}$=$\frac{BM}{BC}$=$\frac{BH}{BO}$��
��$\frac{MH}{2}$=$\frac{\frac{8\sqrt{5}}{5}}{2\sqrt{5}}$=$\frac{BH}{4}$��
��MH=$\frac{8}{5}$��BH=$\frac{16}{5}$��OH=$\frac{4}{5}$��
��M��$\frac{4}{5}$��$\frac{8}{5}$����
��ֱ��ON�Ľ���ʽΪy=2x��
��$\left\{\begin{array}{l}{y=2x}\\{y=-\frac{1}{2}{x}^{2}+\frac{3}{2}x+2}\end{array}\right.$�����$\left\{\begin{array}{l}{x=\frac{-1+\sqrt{17}}{2}}\\{y=-1+\sqrt{17}}\end{array}\right.$����$\left\{\begin{array}{l}{x=\frac{-1-\sqrt{17}}{2}}\\{y=-1-\sqrt{17}}\end{array}\right.$��
��N��$\frac{-1+\sqrt{17}}{2}$��-1+$\sqrt{17}$����
��S��OBN=$\frac{1}{2}$��4����-1+$\sqrt{17}$��=-2+2$\sqrt{17}$��
��2������ͼ2�У�����BED=90��ʱ����BED�ס�BCA��
��BE��DE=BC��AC=2��1��
��DH��y����H��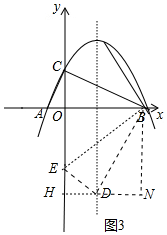
��֤��DHE�ס�EOB��
��OE��DH=BE��DE=2��1��
��DH=$\frac{3}{2}$��
��OE=3��EH=$\frac{1}{2}$OB=2��
��D��$\frac{3}{2}$��-5����
����ͼ3�У�����EDB=90��ʱ����BDE�ס�BCA��
��BD��DE=BC��AC=2��1��
��DH��y����H��BN��DH��N��
�ɡ�HDE�ס�NBD���ɵ�BN��DH=BD��DE=2��1��
��BN=3��
��D��$\frac{3}{2}$��-3����
�������������������ĵ�D������Ϊ��$\frac{3}{2}$��-5����$\frac{3}{2}$��-3����
���� ���⿼����κ����ۺ��⡢���������ε��ж������ʡ�һ�κ��������ʵ�֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ��������������ν�����⣬ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
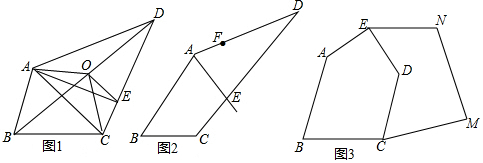
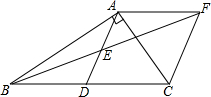 ��Rt��ABC�У���BAC=90�㣬D��BC���е㣬E��AD���е㣬����A��AF��BC��BE���ӳ����ڵ�F��
��Rt��ABC�У���BAC=90�㣬D��BC���е㣬E��AD���е㣬����A��AF��BC��BE���ӳ����ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
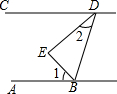 ��ͼ��ʾ��BE�ǡ�ABD��ƽ���ߣ�DE�ǡ�BDC��ƽ���ߣ��ҡ�1+��2=90�㣬��ôֱ��AB��CD��λ�ù�ϵ��Σ���˵�����ɣ�
��ͼ��ʾ��BE�ǡ�ABD��ƽ���ߣ�DE�ǡ�BDC��ƽ���ߣ��ҡ�1+��2=90�㣬��ôֱ��AB��CD��λ�ù�ϵ��Σ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
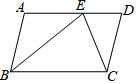 ��ͼ����ƽ���ı���ABCD�У�EΪAD��һ�㣬AB=AE��CE=CD������ECD=30�㣬���ABE=37.5�㣮
��ͼ����ƽ���ı���ABCD�У�EΪAD��һ�㣬AB=AE��CE=CD������ECD=30�㣬���ABE=37.5�㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com