
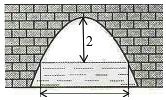
 如图,抛物线形拱桥,当拱顶离水面2m时,水面宽4m.
如图,抛物线形拱桥,当拱顶离水面2m时,水面宽4m.分析 (1)以AB所在直线为x轴、AB的中垂线为y轴建立平面直角坐标系,由图可得顶点C的坐标;
(2)设顶点式y=ax2+2,将A(-2,0)代入求得函数解析式,继而可求得y=-1时x的值,从而得出答案;
(3)根据题意可知,根据x=$\frac{1}{2}$w时,拱顶离水面h=2-y可得答案.
解答 解:(1)如图,以AB所在直线为x轴、AB的中垂线为y轴建立平面直角坐标系,
则抛物线顶点C坐标为(0,2);
(2)设顶点式y=ax2+2,代入A点坐标(-2,0),
得出:a=-0.5,
∴抛物线解析式为y=-0.5x2+2,
当y=-1时,-0.5x2+2=-1,
解得:x=-$\sqrt{6}$或x=$\sqrt{6}$,
∴当水面下降1m,此时水面的宽度是2$\sqrt{6}$m;
(3)根据题意,当x=$\frac{1}{2}$w时,y=-0.5×($\frac{1}{2}$w)2+2=-$\frac{1}{8}$w2+2,
∴此时拱顶离水面h=2-y=2-(-$\frac{1}{8}$w2+2)=$\frac{1}{8}$w2.
点评 本题主要考查二次函数的实际应用能力,根据题意建立合适的平面直角坐标系是解题的根本,理解题意将实际问题转化为二次函数的问题求解是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1.2×109 | B. | 12×108 | C. | 12×1010 | D. | 12×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图线段AB和CD分别表示甲、乙两幢楼的高,AB⊥BD于点B,CD⊥BD于点D,从甲楼A处测得乙楼顶部C的仰角α=30°,测得乙楼底部点D的俯角β=60°,且AB=24米,则CD为( )米.
如图线段AB和CD分别表示甲、乙两幢楼的高,AB⊥BD于点B,CD⊥BD于点D,从甲楼A处测得乙楼顶部C的仰角α=30°,测得乙楼底部点D的俯角β=60°,且AB=24米,则CD为( )米.| A. | 34 | B. | 36 | C. | 32 | D. | 24+8$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
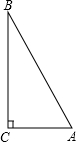 如图,在Rt△ABC中,∠C=90°.
如图,在Rt△ABC中,∠C=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形AEBF中,AB、EF相交于点O,C、D分别是OE、OF的中点.
如图,在平行四边形AEBF中,AB、EF相交于点O,C、D分别是OE、OF的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知AB是⊙O的弦,AB=BC,BD平分∠ABC交⊙O于点D,连接AD,AD=DB.
已知AB是⊙O的弦,AB=BC,BD平分∠ABC交⊙O于点D,连接AD,AD=DB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com