
【题目】二次函数![]() 的图象如图所示,对称轴是直线
的图象如图所示,对称轴是直线![]() ,有以下结论:①
,有以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论的个数是( )
.其中正确的结论的个数是( )
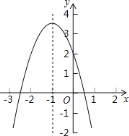
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
由抛物线开口方向得到a<0,由抛物线的对称轴方程得到为b=2a<0,由抛物线与y轴的交点位置得到c>0,则可对①进行判断;根据抛物线与x轴交点个数得到△=b2-4ac>0,则可对②进行判断;利用b=2a可对③进行判断;利用x=-1时函数值为正数可对④进行判断.
解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=-![]() =-1,
=-1,
∴b=2a<0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc>0,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,所以②正确;
∵b=2a,
∴2a-b=0,所以③错误;
∵抛物线开口向下,x=-1是对称轴,所以x=-1对应的y值是最大值,
∴a-b+c>2,所以④正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图(1),AB=7cm,AC⊥AB,BD⊥AB 垂足分别为 A、B,AC=5cm.点P 在线段 AB 上以 2cm/s 的速度由点 A 向点B 运动,同时,点 Q 在射线 BD 上运动.它们运 动的时间为 t(s)(当点 P 运动结束时,点 Q 运动随之结束).
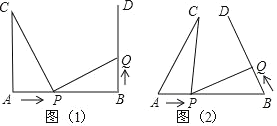
(1)若点 Q 的运动速度与点 P 的运动速度相等,当 t=1 时,△ACP 与△BPQ 是否全等, 并判断此时线段 PC 和线段 PQ 的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB” 改为 “∠CAB=∠DBA=60°”,点 Q 的运动速 度为 x cm/s,其他条件不变,当点 P、Q 运动到某处时,有△ACP 与△BPQ 全等,求出相应的 x、t 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.

(1)求证:AE=DE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师用![]() 个
个![]() 的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边
的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边![]() 共享,或有一面
共享,或有一面![]() 共享.老师拿出一张
共享.老师拿出一张![]() 的方格纸(如图②),请小荣将此
的方格纸(如图②),请小荣将此![]() 个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有________种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有________种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
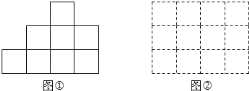
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,CD为△ABC的中线,点E在CD上,且∠AED=∠BCD.

(1)求证:AE=BC.
(2)如图2,连接BE,若AB=AC=2DE,∠CBE=14°,则∠ACD的度数为 (直接写出结果),
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销的一种进价为每件![]() 元的运动休闲杉热销.据市场调查分析,若每件按
元的运动休闲杉热销.据市场调查分析,若每件按![]() 元销售出
元销售出![]() 件;销售单价每涨价
件;销售单价每涨价![]() 元,月销售量就减少
元,月销售量就减少![]() 件.针对这种运动休闲杉的销售情况,请解答以下问题:
件.针对这种运动休闲杉的销售情况,请解答以下问题:
![]() 设销售单价为每件
设销售单价为每件![]() 元,月销售利润为
元,月销售利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式(不必写出
之间的函数关系式(不必写出![]() 的取值范围);
的取值范围);
![]() 商店想使月销售利润达到
商店想使月销售利润达到![]() 元,并使销售量尽量大,请问该休闲杉的销售单价应定为多少元?
元,并使销售量尽量大,请问该休闲杉的销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(1)直接写出一次函数y=kx+b的表达式和反比例函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)求证:AD=BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)是由抛物线y=﹣x2+x+2先作关于y轴的轴对称图形,再将所得到的图象向下平移3个单位长度得到的,点Q1(﹣2.25,q1),Q2(1.5,q2)都在抛物线y=ax2+bx+c(a≠0)上,则q1,q2的大小关系是( )
A. q1>q2 B. q1<q2 C. q1=q2 D. 无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com