
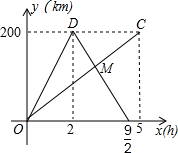
 甲、乙两车分别从相距200千米的A、B两地同时出发相向而行,甲到B地后立即返回,乙到A地后停止行驶,下图是它们离各自出发地的距离y(km)与行驶时间x(h)之间的函数图象.
甲、乙两车分别从相距200千米的A、B两地同时出发相向而行,甲到B地后立即返回,乙到A地后停止行驶,下图是它们离各自出发地的距离y(km)与行驶时间x(h)之间的函数图象. 时,设y=kx+b,则
时,设y=kx+b,则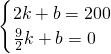 ,
,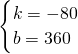 ,
, ;
;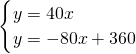 ,
, ,
, ;
; 小时和4小时甲乙两车相遇.
小时和4小时甲乙两车相遇. 两段,利用待定系数法求一次函数解析式解答;
两段,利用待定系数法求一次函数解析式解答;

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 9 | 2 |
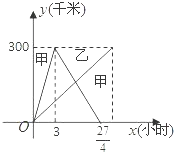 (千米)与行驶时间x(小时)之间的函数关系式,写出自变量的取值范围;
(千米)与行驶时间x(小时)之间的函数关系式,写出自变量的取值范围;查看答案和解析>>
科目:初中数学 来源: 题型:
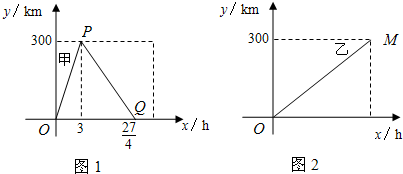
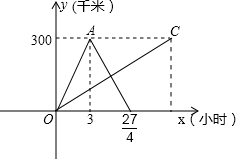 为了参观上海世博会,某公司安排甲、乙两车分别从相距300千米的上海、泰州两地同时出发相向而行,甲到泰州带客后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
为了参观上海世博会,某公司安排甲、乙两车分别从相距300千米的上海、泰州两地同时出发相向而行,甲到泰州带客后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:
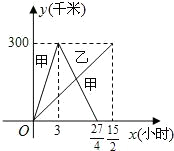 ,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:
| 9 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com