
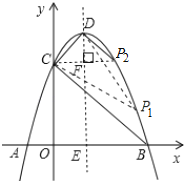
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),
∴根据题意,得![]() ,
,
解得![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3.
(2)
解:由y=﹣x2+2x+3得,D点坐标为(1,4),
∴CD=![]() =
=![]() ,
,
BC=![]() =3
=3![]() ,
,
BD=![]() =2
=2![]() ,
,
∵CD2+BC2=(![]() )2+(3
)2+(3![]() )2=20,BD2=(2
)2=20,BD2=(2![]() )2=20,
)2=20,
∴CD2+BC2=BD2,
∴△BCD是直角三角形;
(3)
解:存在.
y=﹣x2+2x+3对称轴为直线x=1.
①若以CD为底边,则P1D=P1C,
设P1点坐标为(x,y),根据勾股定理可得P1C2=x2+(3﹣y)2,P1D2=(x﹣1)2+(4﹣y)2,
因此2+(3﹣y)2=(x﹣1)2+(4﹣y)2,
即y=4﹣x.
又P1点(x,y)在抛物线上,
∴4﹣x=﹣x2+2x+3,
即x2﹣3x+1=0,
解得x1=![]() ,x2=
,x2=![]() <1,应舍去,
<1,应舍去,
∴x=![]() ,
,
∴y=4﹣x=![]() ,
,
即点P1坐标为(![]() ,
,![]() ).
).
②若以CD为一腰,
∵点P2在对称轴右侧的抛物线上,由抛物线对称性知,点P2与点C关于直线x=1对称,
此时点P2坐标为(2,3).
∴符合条件的点P坐标为(![]() ,
,![]() )或(2,3).
)或(2,3).
【解析】(1)将A(﹣1,0)、B(3,0)代入二次函数y=ax2+bx﹣3a求得a、b的值即可确定二次函数的解析式;
(2)分别求得线BC、CD、BD的长,利用勾股定理的逆定理进行判定即可;
(3)分以CD为底和以CD为腰两种情况讨论.运用两点间距离公式建立起P点横坐标和纵坐标之间的关系,再结合抛物线解析式即可求解.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(1)求此抛物线的解析式;
(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标;
(3)当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时,是否存在使△BDE为直角三角形的情况,若存在,请直接写出符合要求的E点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师家距学校1900米,某天他步行去上班,走到路程的一半时发现忘带手机,此时离上班时间还有23分钟,于是他立刻步行回家取手机,随后骑电瓶车返回学校.已知李老师骑电瓶车到学校比他步行到学校少用20分钟,且骑电瓶车的平均速度是步行速度的5倍,李老师到家开门、取手机、启动电瓶车等共用4分钟.
(1)求李老师步行的平均速度;
(2)请你判断李老师能否按时上班,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子x+ ![]() (x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是
(x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是 ![]() ,矩形的周长是2(x+
,矩形的周长是2(x+ ![]() );当矩形成为正方形时,就有x=
);当矩形成为正方形时,就有x= ![]() (x>0),解得x=1,这时矩形的周长2(x+
(x>0),解得x=1,这时矩形的周长2(x+ ![]() )=4最小,因此x+
)=4最小,因此x+ ![]() (x>0)的最小值是2.模仿张华的推导,你求得式子
(x>0)的最小值是2.模仿张华的推导,你求得式子 ![]() (x>0)的最小值是( )
(x>0)的最小值是( )
A.2
B.1
C.6
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)计算:( ![]() ﹣2)0+(﹣1)2014+
﹣2)0+(﹣1)2014+ ![]() ﹣sin45°;
﹣sin45°;
(2)先化简,再求值:(a2b+ab)÷ ![]() ,其中a=
,其中a= ![]() +1,b=
+1,b= ![]() ﹣1.
﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习成为现代人的时尚,某市有关部门统计了最近6个月到图书馆的读者的职业分布情况,并做了下列两个不完整的统计图. 
(1)在统计的这段时间内,共有万人次到图书馆阅读,其中商人占百分比为%;
(2)将条形统计图补充完整;
(3)若5月份到图书馆的读者共28000人次,估计其中约有多少人次读者是职工?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=45°,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,连接CF,则下列结论:①BF=AC; ②∠FCD=45°; ③若BF=2EC,则△FDC周长等于AB的长;其中正确的有( )
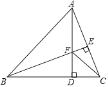
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com