练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图19-3-18所示，等腰△ABC中，AB=AC，点E、F分别是AB、AC的中点，CE⊥BF于点O.求证:

    图19-3-18

    (1)四边形EFCB是等腰梯形;

    (2)EF2+BC2=2BE2.
    答案：
    解析：

    		 思路分析：(1)根据三角形中位线定理可证四边形EFCB是梯形，再由等腰三角形的性质可证四边形EFCB是等腰梯形;

    (2)由勾股定理可证出关系式.

    证明:(1)因为点E、F分别是AB、AC的中点，所以EF∥BC，显然BE与CF不平行，所以四边形EFCB是梯形.因为AB=AC，所以∠ABC=∠ACB.所以梯形EFCB是等腰梯形.

    (2)在Rt△OEF中，由勾股定理，得EF2=OE2+OF2. ①

    同理，BC2=OB2+OC2. ②

    ①+②，得EF2+BC2=(OE2+OB2)+(OF2+OC2)=2BE2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

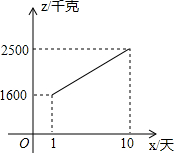    （2012•重庆模拟）樱桃含铁量位于各种水果之首，常食樱桃可促进血红蛋白再生，既可防治缺铁性贫血，又可增强体质，健脑益智．樱桃营养丰富，具有调中益气，健脾和胃，祛风湿，“令人好颜色，美志性”之功效，对食欲不振，消化不良，风湿身痛等症状均有益处，今年4月份，某樱桃种植基地种植的樱桃喜获丰收，4月1日至10日，销售价格y（元/千克）与天数x（天）（1≤x≤10且x为整数）的函数关系如下表：
    天数x 1 2 3 4 5 6 7 8 9 10
    市场价格y 19.5 19 18.5 18 17.5 17 16.5 16 15.5 15
    销售量z（千克）与天数x（天）（1≤x≤10且x为整数）之间存在如图所示的变化趋势；
    （1）请观察题中的表格，用所学过的一次函数，反比例函数或二次函数的有关知识，直接写出y与x之间的函数关系式，根据如图所示的变化趋势，直接写出z与x之间满足的一次函数关系式；
    （2）若采摘樱桃的人员费用m（元）与销售量z（千克）之间的函数关系式为：m=0.1z+100．则4月份前10天，哪天销售樱桃的利润最大，求出这个最大利润；
    （3）在（1）问的基础上，4月11日至4月12日，该樱桃种植基地调整了销售价格，每天都比前一天增加a%（0＜a＜20），在此影响下，销售量每天都比前一天减少100千克，若这两天销售樱桃的利润为80330元，请你参考以下数据，通过计算估算出整数值．
    （参考数据：742=5476，74.52=5550.25，752=5625）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示是2003年11月的日历表．
    星期日 星期一 星期二 星期三 星期四 星期五 星期六
    1 2 3 4 5 6 7
    8 9 10 11 12 13 14
    15 16 17 18 19 20 21
    22 23 24 25 26 27 28
    29 30
    请回答下列问题：
    （1）若一竖列的三个数的和为42，这三个数分别是多少？若和为44，能求出这三天是几号吗？为什么？
    （2）若一竖列的四个数之和为74，这四个数分别是多少？四个数的和能不能是75，为什么？
    （3）如果是2×2的矩形块的四个数的和为80，求出这四个数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    如图19-1-18所示，ABCD中，点E在AD上，以BE为折痕，将△ABE向上翻折，点A正好落在CD上的点F处.若△FDE的周长为8，△FCB的周长为22，求FC的长.

    图19-1-18

    查看答案和解析>>

    科目：初中数学 来源：湖北省期末题 题型：解答题

    如图（1）的矩形包书纸示意图中，虚线是折痕，阴影是裁剪掉的部分，四角均为大小相同的正方形，正方形的边长为折叠进去的宽度。
    （1）如图（2）数学课本长为26㎝，宽为18.5㎝，厚为1㎝小明用一张面积为1260㎝2的矩形纸包好了这本书，展开后如图（1）所示，求折叠进去的宽度。
    （2）现有一本长为19㎝，宽为16㎝，厚为6㎝的字典，你能用一张41㎝×26㎝的矩形纸，按图（1）所示的方法包好这本字典，并使折叠进去的宽度不小于3㎝吗？请说明理由。

    图（1）                      图（2）

    查看答案和解析>>

    同步练习册答案