
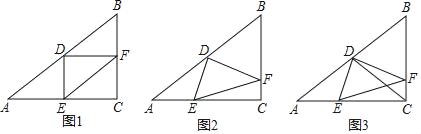
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”÷ABCÖŠ£¬”ĻACB=90”ć£¬AC=8£¬cosA=![]() £¬DŹĒAB±ßµÄÖŠµć£¬EŹĒAC±ßÉĻŅ»µć£¬ĮŖ½įDE£¬¹żµćD×÷DF”ĶDE½»BC±ßÓŚµćF£¬ĮŖ½įEF£®
£¬DŹĒAB±ßµÄÖŠµć£¬EŹĒAC±ßÉĻŅ»µć£¬ĮŖ½įDE£¬¹żµćD×÷DF”ĶDE½»BC±ßÓŚµćF£¬ĮŖ½įEF£®
£Ø1£©ČēĶ¼1£¬µ±DE”ĶACŹ±£¬ĒóEFµÄ³¤£»
£Ø2£©ČēĶ¼2£¬µ±µćEŌŚAC±ßÉĻŅĘ¶ÆŹ±£¬”ĻDFEµÄÕżĒŠÖµŹĒ·ń»į·¢Éś±ä»Æ£¬Čē¹ū±ä»ÆĒėĖµ³ö±ä»ÆĒéæö£»Čē¹ū±£³Ö²»±ä£¬ĒėĒó³ö”ĻDFEµÄÕżĒŠÖµ£»
£Ø3£©ČēĶ¼3£¬ĮŖ½įCD½»EFÓŚµćQ£¬µ±”÷CQFŹĒµČŃüČż½ĒŠĪŹ±£¬ĒėÖ±½ÓŠ“³öBFµÄ³¤£®
”¾“š°ø”æ£Ø1£©EF=5£»£Ø2£©²»±ä£¬ĄķÓɼū½āĪö£»£Ø3£©BFµÄ³¤ĪŖ3»ņ![]() »ņ
»ņ![]() £®
£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ÓÉcosA=![]() £¬øł¾ŻČń½ĒČż½ĒŗÆŹżµÄ¶ØŅåæÉĒóæÉĒóAC=8£¬AE=4£¬ŌŚRt”÷EDFÖŠ£¬Óɹ“¹É¶ØĄķĒó³öDE=3£¬ŌŚRt”÷AEDÖŠ£¬Óɹ“¹É¶ØĄķĒó³öEFµÄ³¤£»
£¬øł¾ŻČń½ĒČż½ĒŗÆŹżµÄ¶ØŅåæÉĒóæÉĒóAC=8£¬AE=4£¬ŌŚRt”÷EDFÖŠ£¬Óɹ“¹É¶ØĄķĒó³öDE=3£¬ŌŚRt”÷AEDÖŠ£¬Óɹ“¹É¶ØĄķĒó³öEFµÄ³¤£»
£Ø2£©¹żµćD×÷DH”ĶAC£¬DG”ĶBC£¬“¹×ć·Ö±šĪŖµćH”¢G£¬ÓÉ£Ø1£©æɵĆDH=3£¬DG=4£¬ŌŁÖ¤”÷EDH”×”÷FDG£¬µĆµ½![]() ,Č»ŗóøł¾ŻÕżĒŠ¶ØŅåĒó½ā£»
,Č»ŗóøł¾ŻÕżĒŠ¶ØŅåĒó½ā£»
£Ø3£©·ÖQF=QC£¬FQ=FC£¬CF=CQČżÖÖĒéæöĒó½ā.
½ā£ŗ£Ø1£©”ß”ĻACB=90”ć£¬![]()
”ą![]() £¬
£¬
”ßAC=8£¬
”ąAB=10£¬
”ßDŹĒAB±ßµÄÖŠµć£¬
”ą![]() £¬
£¬
”ßDE”ĶAC£¬
”ą”ĻDEA=”ĻDEC=90”ć£¬
”ą![]() £¬
£¬
”ąAE=4£¬
”ąCE=8©4=4£¬
”ßŌŚRt”÷AEDÖŠ£¬AE2+DE2=AD2£¬
”ąDE=3£¬
”ßDF”ĶDE£¬
”ą”ĻFDE=90”ć£¬
Ó֔ߔĻACB=90”ć£¬
”ąĖıߊĪDECFŹĒ¾ŲŠĪ£¬
”ąDF=EC=4£¬
”ßŌŚRt”÷EDFÖŠ£¬DF2+DE2=EF2£¬
”ąEF=5
£Ø2£©²»±ä
ČēĶ¼2£¬
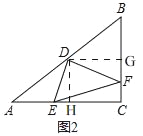
¹żµćD×÷DH”ĶAC£¬DG”ĶBC£¬“¹×ć·Ö±šĪŖµćH”¢G£¬
ÓÉ£Ø1£©æɵĆDH=3£¬DG=4£¬
”ßDH”ĶAC£¬DG”ĶBC£¬
”ą”ĻDHC=”ĻDGC=90”ć
Ó֔ߔĻACB=90”ć£¬
”ąĖıߊĪDHCGŹĒ¾ŲŠĪ£¬
”ą”ĻHDG=90”ć£¬
”ß”ĻFDE=90”ć£¬
”ą”ĻHDG©”ĻHDF=”ĻEDF©”ĻHDF£¬
¼“”ĻEDH=”ĻFDG£¬
Ó֔ߔĻDHE=”ĻDGF=90”ć
”ą”÷EDH”×”÷FDG£¬
”ą![]() £¬
£¬
”ß”ĻFDE=90”ć£¬
”ą![]() £¬
£¬
£Ø3£©¢Łµ±QF=QCŹ±£¬
”ą”ĻQFC=”ĻQCF£¬
”ß”ĻEDF+”ĻECF=180”ć£¬
”ąµćD£¬E£¬C£¬FĖÄµć¹²Ō²£¬
”ą”ĻECQ=”ĻDFE£¬”ĻDFE+”ĻQFC=”ĻECQ+”ĻQCF=”ĻACB=90”ć£¬
¼“”ĻDFC=90”ć£¬
Ó֔ߔĻACB=90”ć£¬DŹĒABµÄÖŠµć£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
¢Śµ±FQ=FCŹ±£¬
”ą”ĻBCD=”ĻCQF£¬
”ßµćDŹĒABµÄÖŠµć£¬
”ąBD=CD=![]() AB=5£¬
AB=5£¬
”ą”ĻBDC=”ĻBCD£¬
”ą”ĻBCD=”ĻFCQ£¬”ĻBDC=”ĻCFQ£¬
”ą”÷FQC”×”÷DCB£¬
ÓÉ¢ŁÖŖ£¬µćD£¬E£¬C£¬FĖÄµć¹²Ō²£¬
”ą”ĻDEF=”ĻDCF£¬
”ß”ĻDQE=”ĻFQC£¬
”ą”÷FQC”×”÷DEQ£¬
¼“£ŗ”÷FQC”×”÷DEQ”×”÷DCB
”ßŌŚRt”÷EDFÖŠ£¬![]() £¬
£¬
”ąÉčDE=3k£¬ŌņDF=4k£¬EF=5k£¬
”ß”ĻDEF=”ĻDCF=”ĻCQF=”ĻDQE£¬
”ąDE=DQ=3k£¬
”ąCQ=5©3k£¬
”ß”÷DEQ”×”÷DCB£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ß”÷FQC”×”÷DCB£¬
”ą![]() £¬
£¬
”ą £¬
£¬
½āµĆ![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
¢Ūµ±CF=CQŹ±£¬ČēĶ¼3£¬
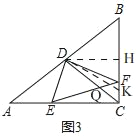
”ą”ĻBCD=”ĻCQF£¬
ÓÉ¢ŚÖŖ£¬CD=BD£¬
”ą”ĻBDC=”ĻBCD£¬
”ß”÷EDQ”×”÷BDK£¬
ŌŚBC±ßÉĻ½ŲČ”BK=BD=5£¬¹żµćD×÷DH”ĶBCÓŚH£¬
”ąDH=![]() AC=4£¬BH=
AC=4£¬BH=![]() BC=3£¬Óɹ“¹É¶ØĄķµĆ
BC=3£¬Óɹ“¹É¶ØĄķµĆ![]() £¬
£¬
Ķ¬¢ŚµÄ·½·ØµĆ£¬”÷CFQ”×”÷EDQ£¬
”ąÉčDE=3m£¬ŌņEQ=3m£¬EF=5m£¬
”ąFQ=2m£¬
”ß”÷EDQ”×”÷BDK£¬
”ą![]() £¬
£¬
”ąDQ=![]() m£¬
m£¬
”ąCQ=FC=5©![]() m£¬
m£¬
”ß”÷CQF”×”÷BDK£¬
”ą![]() £¬
£¬
”ą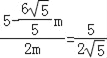 £¬
£¬
½āµĆm=![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £®
£®
¼“£ŗ”÷CQFŹĒµČŃüČż½ĒŠĪŹ±£¬BFµÄ³¤ĪŖ3»ņ![]() »ņ
»ņ![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔Ć÷¼ŅµÄ½ÅĢ¤Ź½Ą¬»ųĶ°ČēĶ¼£¬µ±½Å²ČĢ¤°åŹ±Ą¬»ųĶ°øĒ“ņæŖ×ī“óÕŽĒ”ĻABC =45”ć£¬ĪŖ½ŚŹ”¼ŅĄļæռ䊔Ć÷ Ļė°ŃĄ¬»ųĶ°·Åµ½×ĄĻĀ£¬¾²āĮæץ×ÓĻĀŃŲĄėµŲĆęøß 55cm£¬Ą¬»ųĶ°øß BD=33.1cm£¬Ķ°øĒÖ±¾¶ BC=28.2cm£¬ĪŹĄ¬»ųĶ°·Åµ½×ĄĻĀ²ČĢ¤°åŹ±£¬Ķ°øĒĶźČ«“ņæŖӊƻӊÅöµ½×Ą×ÓĻĀŃŲ£æ(![]() 1.41 )
1.41 )

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬CŹĒ”ŃOÉĻŅ»µć£¬DŌŚABµÄŃÓ³¤ĻßÉĻ£¬ĒŅ”ĻBCD=”ĻA£®
£Ø1£©ĒóÖ¤£ŗCDŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©Čō”ŃOµÄ°ė¾¶ĪŖ3£¬CD=4£¬ĒóBDµÄ³¤£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±ĻßABÓėCDĻą½»ÓŚµćO£¬OF£¬OD·Ö±šŹĒ”ĻAOE£¬”ĻBOEµÄĘ½·ÖĻߣ®

(1)Š“³ö”ĻDOEµÄ²¹½Ē£»
(2)Čō”ĻBOE£½62”ć£¬Ēó”ĻAODŗĶ”ĻEOFµÄ¶ČŹż£»
(3)ŹŌĪŹÉäĻßODÓėOFÖ®¼äÓŠŹ²Ć“ĢŲŹāµÄĪ»ÖĆ¹ŲĻµ£æĪŖŹ²Ć“£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ½ńÄź”°ĀĢÉ«ĒåĆ÷£¬ĪÄĆ÷¼Ąģė”±»ī¶ÆÖŠ£¬Ä³»ØµźÓĆ![]() ŌŖ¹ŗ½ųČōøɾջأ¬ŗÜæģŹŪĶź£¬½Ó×ÅÓÖÓĆ
ŌŖ¹ŗ½ųČōøɾջأ¬ŗÜæģŹŪĶź£¬½Ó×ÅÓÖÓĆ![]() ŌŖ¹ŗ½ųµŚ¶žÅś¾Õ»Ø£¬ŅŃÖŖµŚ¶žÅśĖł¹ŗ½ų¾Õ»ØµÄŹżĮæŹĒµŚŅ»ÅśĖł¹ŗ½ų¾Õ»ØŹżĮæµÄ
ŌŖ¹ŗ½ųµŚ¶žÅś¾Õ»Ø£¬ŅŃÖŖµŚ¶žÅśĖł¹ŗ½ų¾Õ»ØµÄŹżĮæŹĒµŚŅ»ÅśĖł¹ŗ½ų¾Õ»ØŹżĮæµÄ![]() ±¶£¬ĒŅĆæ¶ä¾Õ»ØµÄ½ų¼Ū±ČµŚŅ»ÅśĆæ¶ä¾Õ»ØµÄ½ų¼Ū¶ą
±¶£¬ĒŅĆæ¶ä¾Õ»ØµÄ½ų¼Ū±ČµŚŅ»ÅśĆæ¶ä¾Õ»ØµÄ½ų¼Ū¶ą![]() ŌŖ.
ŌŖ.
£Ø1£©ĒóµŚŅ»ÅśĆæ¶äĘæ¾Õ»ØµÄ½ų¼ŪŹĒ¶ąÉŁŌŖ£æ
£Ø2£©ČōµŚŅ»ÅśĆæ¶ä¾Õ»Ø°“![]() ŌŖŹŪ¼ŪĻśŹŪ£¬ŅŖŹ¹×ÜĄūČó²»µĶÓŚ
ŌŖŹŪ¼ŪĻśŹŪ£¬ŅŖŹ¹×ÜĄūČó²»µĶÓŚ![]() ŌŖ£Ø²»æ¼ĀĒĘäĖūŅņĖŲ£©£¬µŚ¶žÅśĆæ¶ä¾Õ»ØµÄŹŪ¼ŪÖĮÉŁŹĒ¶ąÉŁŌŖ£æ
ŌŖ£Ø²»æ¼ĀĒĘäĖūŅņĖŲ£©£¬µŚ¶žÅśĆæ¶ä¾Õ»ØµÄŹŪ¼ŪÖĮÉŁŹĒ¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻACB=90”ć£¬AC=30cm£¬BC=40cm£®µćP“ÓµćA³ö·¢£¬ŅŌ5cm/sµÄĖŁ¶ČŃŲACĻņÖÕµćCŌČĖŁŅĘ¶Æ£®¹żµćP×÷PQ”ĶAB£¬“¹×ćĪŖµćQ£¬ŅŌPQĪŖ±ß×÷Õż·½ŠĪPQMN£¬µćMŌŚAB±ßÉĻ£¬Į¬½ÓCN£®ÉčµćPŅĘ¶ÆµÄŹ±¼äĪŖt£Øs£©£®

£Ø1£©PQ=______£»£ØÓĆŗ¬tµÄ“śŹżŹ½±ķŹ¾£©
£Ø2£©µ±µćN·Ö±šĀś×ćĻĀĮŠĢõ¼žŹ±£¬Ēó³öĻąÓ¦µÄtµÄÖµ£»¢ŁµćC£¬N£¬MŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£»¢ŚµćNĀäŌŚBC±ßÉĻ£»
£Ø3£©µ±”÷PCNĪŖµČŃüČż½ĒŠĪŹ±£¬ĒótµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ō²ÖłŠĪ²£Į§±£¬øßĪŖ![]() £¬µ×ĆęÖܳ¤ĪŖ
£¬µ×ĆęÖܳ¤ĪŖ![]() £¬ŌŚ±ÄŚĄė±µ×
£¬ŌŚ±ÄŚĄė±µ×![]() µÄµć
µÄµć![]() “¦ÓŠŅ»µĪ·äĆŪ£¬“ĖŹ±Ņ»Ö»ĀģŅĻÕżŗĆŌŚ±Ķā±Ś£¬Ąė±ÉĻŃŲ
“¦ÓŠŅ»µĪ·äĆŪ£¬“ĖŹ±Ņ»Ö»ĀģŅĻÕżŗĆŌŚ±Ķā±Ś£¬Ąė±ÉĻŃŲ![]() Óė·äĆŪĻą¶ŌµÄµć
Óė·äĆŪĻą¶ŌµÄµć![]() “¦£¬ŌņĀģŅĻµ½“ļ·äĆŪµÄ×ī¶Ģ¾ąĄėĪŖ( )
“¦£¬ŌņĀģŅĻµ½“ļ·äĆŪµÄ×ī¶Ģ¾ąĄėĪŖ( )![]() .
.
A. 15B. ![]() C. 12D. 18
C. 12D. 18
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy£½2x+6½»xÖįÓŚA£¬½»yÖįÓŚB£®

£Ø1£©Ö±½ÓŠ“³öA£Ø”” ””£¬”” ””£©£¬B£Ø”” ””£¬”” ””£©£»
£Ø2£©ČēĶ¼1£¬µćEĪŖÖ±Ļßy£½x+2ÉĻŅ»µć£¬µćFĪŖÖ±Ļßy£½![]() xÉĻŅ»µć£¬ČōŅŌA£¬B£¬E£¬FĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬ĒóµćE£¬FµÄ×ų±ź
xÉĻŅ»µć£¬ČōŅŌA£¬B£¬E£¬FĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬ĒóµćE£¬FµÄ×ų±ź
£Ø3£©ČēĶ¼2£¬µćC£Øm£¬n£©ĪŖĻ߶ĪABÉĻŅ»¶Æµć£¬D£Ø©7m£¬0£©ŌŚxÖįÉĻ£¬Į¬½ÓCD£¬µćMĪŖCDµÄÖŠµć£¬ĒóµćMµÄׯ×ų±źyŗĶŗį×ų±źxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ö±½ÓŠ“³öŌŚµćCŅĘ¶Æ¹ż³ĢÖŠµćMµÄŌĖ¶ÆĀ·¾¶³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
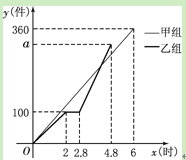
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½×鹤ČĖĶ¬Ź±¼Ó¹¤Ä³ÖÖĮć¼ž£¬ŅŅ×鹤×÷ÖŠÓŠŅ»“ĪĶ£²śøü»»Éč±ø£¬øü»»Éč±ø
ŗó£¬ŅŅ×éµÄ¹¤×÷Š§ĀŹŹĒŌĄ“µÄ2±¶£®Į½×éø÷×Ō¼Ó¹¤Įć¼žµÄŹżĮæ![]() (¼ž)ÓėŹ±¼ä
(¼ž)ÓėŹ±¼ä![]() (Ź±)µÄŗÆŹżĶ¼
(Ź±)µÄŗÆŹżĶ¼
ĻóČēĶ¼ĖłŹ¾£®
£Ø1£©Ēó¼××é¼Ó¹¤Įć¼žµÄŹżĮæyÓėŹ±¼ä![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®£Ø2·Ö£©
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®£Ø2·Ö£©
£Ø2£©ĒóŅŅ×é¼Ó¹¤Įć¼ž×ÜĮæ![]() µÄÖµ£®£Ø3·Ö£©
µÄÖµ£®£Ø3·Ö£©
£Ø3£©¼×”¢ŅŅĮ½×é¼Ó¹¤³öµÄĮć¼žŗĻŌŚŅ»Ęš×°Ļ䣬Ćæ¹»300¼ž×°Ņ»Ļ䣬Įć¼ž×°ĻäµÄŹ±¼äŗöĀŌ²»¼Ę£¬Ēó¾¹ż¶ą³¤Ź±¼äĒ”ŗĆ×°ĀśµŚ1Ļä£æŌŁ¾¹ż¶ą³¤Ź±¼äĒ”ŗĆ×°ĀśµŚ2Ļä£æ£Ø5·Ö£©
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com