
如图,已知直线y=-x+4与反比例函数y=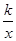 的图象相交于点A(-2,a),并且与x轴相交于点B。
的图象相交于点A(-2,a),并且与x轴相交于点B。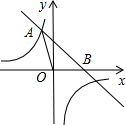
(1)求a的值;
(2)求反比例函数的表达式;
(3)求△AOB的面积。
(1)6;(2) y=-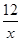 ;(3)12.
;(3)12.
解析试题分析:(1)要求a的值很简单的直接将坐标点A代入一次函数解析式中即可可求得a值;(2)要求反比例函数解析式就要和第(1)问中求得a值,即求得点A的坐标,已知点A为两个函数的交点,那么就说明这个点也符合反比例函数解析式,代入其中即可求得k的值,那么就求出反比例函数解析式为:y=-;(3)要求三角形的面积,就需要求出三角形的高线,首先就需要作出辅助线段,然后确定以那一条边为底,观察本图可知要以AB为底边求解最好。
试题解析:解:(1)将A(-2,a)代入y=-x+4中,得:a=-(-2)+4,所以a=6,
(2)由(1)得:A(-2,6)
将A(-2,6)代入y=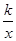 中,得到:6=
中,得到:6=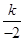 ,即k=-12
,即k=-12
所以反比例函数的表达式为:y=-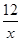 ,
,
(3)如图:过A点作AD⊥x轴于D;
∵A(-2,6),∴AD=6
在直线y=-x+4中,令y=0,得x=4
∴B(4,0),即OB=4
∴△AOB的面积S=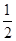 OB×AD=
OB×AD=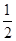 ×4×6=12.
×4×6=12.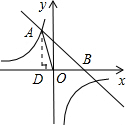
考点:反比例函数综合题.


科目:初中数学 来源: 题型:解答题
如图,梯形ABCD中,AB∥CD,AB=14,AD= 4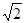 ,CD=7.直线l经过A,D两点,且sin∠DAB=
,CD=7.直线l经过A,D两点,且sin∠DAB=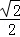 .动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
.动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.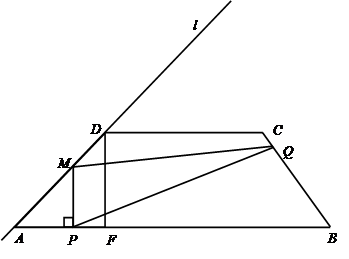
(1)求腰BC的长;
(2)当Q在BC上运动时,求S与t的函数关系式;
(3)在(2)的条件下,是否存在某一时刻t,使得△MPQ的面积S是梯形ABCD面积的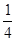 ?若存在,请求出t的值;若不存在,请说明理由;
?若存在,请求出t的值;若不存在,请说明理由;
(4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,
①当C点运动到何处时直线EF∥直线BO?此时⊙F和直线BO的位置关系如何?请说明理由.
②G为CD与⊙F的交点,H为直线DF上的一个动点,连结HG、HC,求HG+HC的最小值,并将此最小值用x表示.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
A、B两码头相距150千米,甲客船顺流由A航行到B,乙客船逆流由B到A,若甲、乙两客船在静水中的速度相同,同时出发,它们航行的路程y(千米)与航行时间x(时)的关系如图所示.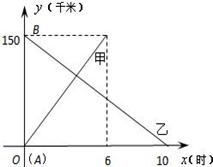
(1)求客船在静水中的速度及水流速度;
(2)一艘货轮由A码头顺流航行到B码头,货轮比客船早2小时出发,货轮在静水中的速度为10千米/时,在此坐标系中画出货轮航程y(千米)与时间x(时)的关系图象,并求货轮与客船乙相遇时距A码头的路程。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地收割小麦,其中30台派往A地,20台派往B地.两地区与该租赁公司商定的每天的租赁价格如下:
| | 甲型收割机的租金 | 乙型收割机的租金 |
| A地 | 1800元/台 | 1600元/台 |
| B地 | 1600元/台 | 1200元/台 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,双曲线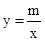 和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.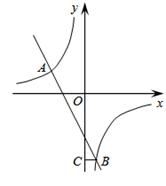
(1)求双曲线和直线的解析式;
(2)直接写出不等式 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知一次函数y=(1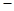 2m)x+m+1,求当m为何值时.
2m)x+m+1,求当m为何值时.
(1)y随x的增大而增大?
(2)图象经过第一、二、四象限?
(3)图象经过第二、四象限?
(4)图象与y轴的交点在x轴的下方?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
“十一黄金周”的某一天,小刚全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩,该小汽车离家的路程S(千米)与时间t (时)的关系可以用右图的折线表示。根据图象提供的有关信息,解答下列问题: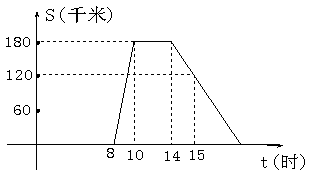
(1)小刚全家在旅游景点游玩了多少小时?
(2)求出整个旅程中S(千米)与时间t (时)的函数关系式,并求出相应自变量t的取值范围。
(3)小刚全家在什么时候离家120㎞?什么时候到家?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元∕台) | 60 | 55 | 50 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com