练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．已知x：y：z=2：3：4，求$\frac{x+y+z}{x-2y+3z}$的值．

    分析 设x=2k，y=3k，z=4k，代入$\frac{x+y+z}{x-2y+3z}$求解即可．

    解答 解：∵x：y：z=2：3：4，
    ∴可设x=2k，y=3k，z=4k，
    ∴$\frac{x+y+z}{x-2y+3z}$=$\frac{2k+3k+4k}{2k-6k+12k}$=$\frac{9k}{8k}$=$\frac{9}{8}$．

    点评 本题主要考查了分式的化简求值，解题的关键是把设出x=2k，y=3k，z=4k．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    17．下列化简正确的是（　　）
    A．$\sqrt{\frac{1}{3}}$=$\frac{\sqrt{3}}{3}$B．$\sqrt{（-5）^{2}}$=-5C．$\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$D．$\sqrt{12}$=4$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．若关于x的一元二次方程kx2+3x-1=0有实数根，则k的取值范围是（　　）
    A．k$≥-\frac{9}{4}$B．k$＞-\frac{9}{4}$C．k$≥-\frac{9}{4}$且k≠0D．k$＞-\frac{9}{4}$且k≠0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

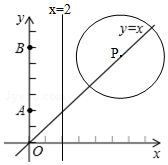    15．如图，在平面直角坐标系xOy中，A（0，2），B（0，6），点P在直线y=x上，⊙P的半径为3，设P（x，y）．
    （1）求⊙P与直线x=2相切时点P的坐标；
    （2）动点C在直线y=x上，若以A、B、C三点为顶点的三角形是等腰三角形，则点C的个数是3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知如图，在△ABC中，∠ACB=90°，△ACE，△CBD都是等边三角形，试判断EC与BD的位置关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知圆内接四边形ABCE中，AB=AC，BC、AE的延长线交于D，求证：AC•CD=AD•CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．解下列方程
    （1）|5x-2|=3
    （2）$\frac{2|x-1|-5}{3}$=1
    （3）|x-1|=-2x+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

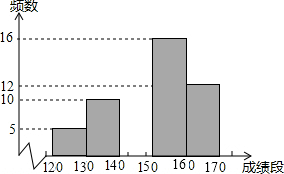    5．为迎接2016年初中学业水体育考试，某校从500名九年级学生中随机抽取部分学生进行1分钟跳绳测试，并把测试成绩进行分析整理，制作成如下统计图表
    成绩段频数频率
    120x13050.1
    130x14010A
    140x150B0.14
    150x16016C
    160x170120.24
    根据图表解决下列问题
    （1）本次共抽取了50名学生进行体育测试，上表中，a=0.2，b=7，c=0.32
    （2）补充完整图所示的条形统计图；
    （3）“跳绳”数在150个以上，则此项成绩可得满分，请你估计今年全校九年级有多少名学生在此项成绩能获满分？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

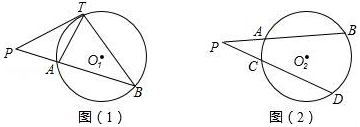
    6．（1）如图（1），PT与⊙O1相切于点T，PAB与⊙O1相交于A、B两点，证明△PTA∽△PBT．
    （2）请应用以上结论解决下列问题：如图（2），PAB、PCD分别与⊙O2相交于A、B、C、D四点，已知PA=2，PB=7，PC=3，求CD的长．

    查看答案和解析>>

    同步练习册答案