
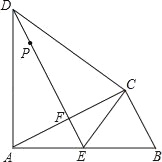
【题目】如图,△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,与AB相交于点E,连接CE.
(1)说明:AE=CE=BE;
(2)若AB=15cm,P是直线DE上的一点.则当P在何处时,PB+PC最小,并求出此时PB+PC的值.
【答案】(1)证明见解析;(2)当点P在E处时,PB+PC=15cm.
【解析】
(1)根据等边三角形“三合一”的性质证得DE垂直平分AC;然后由等腰三角形的判定知AE=CE,根据等边对等角、直角三角形的两个锐角互余的性质以及等量代换求得∠BCE=∠B;最后根据等角对等边证得CE=BE,所以AE=CE=BE;
(2)由(1)知,DE垂直平分AC,故PC=PA;由等量代换知PB+PC=PB+PA;根据两点之间线段最短可知,当点P、B、A在同一直线上最小,所以点P在E处时最小.
(1)在等边三角形ADC中,∵DF⊥AC,∴DF垂直平分AC,∴AE=CE,∴∠ACE=∠CAE(等边对等角);
∵∠ACB=90°(已知),∴∠ACE+∠BCE=∠CAE+∠B=90°,∴∠BCE=∠B,∴CE=BE(等角对等边),∴AE=CE=BE;
(2)由(1)知,DE垂直平分AC,∴PC=PA,∴PB+PC=PB+PA;
∴当PB+PC最小时,也就是PB+PA最小,即点P、B、A在同一直线上最小,所以点P在E处时最小.
当点P在E处时,PB+PC=EB+EC=EB+EA=AB=15cm.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2平移后的位置如图所示,点A,B坐标分别为(﹣1,0)、(3,0),设平移后的抛物线与y轴交于点C,其顶点为D.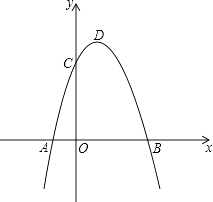
(1)求平移后的抛物线的解析式和点D的坐标;
(2)∠ACB和∠ABD是否相等?请证明你的结论;
(3)点P在平移后的抛物线的对称轴上,且△CDP与△ABC相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题: 
(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图可以近似地刻画下列哪个情景( )
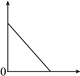
A. 小明匀速步行上学时离学校的距离与时间的关系
B. 匀速行驶的汽车的速度与时间的关系
C. 小亮妈妈到超市购买苹果的总费用与苹果质量的关系
D. 一个匀速上升的气球的高度与时间的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列方程:①![]() ;②0.3x=1;③
;②0.3x=1;③![]() ;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数0,B点表示的数是最小的正整数,C点表示数5,点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.

(1) BC= .
(2) A,B,C在数轴上同时运动,点B和点C分别以每秒3个单位长度和6个单位长度的速度向右运动,点A以每秒a个单位长度的速度向左运动。在运动过程中,3BC-2AB的值始终保持不变,请求出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市场的公平秤如图,把10千克的菜放到秤上,指示盘上的指针转了180°.
(1)如果把2.75千克的菜放在秤上,指针转过多少度?
(2)如果称好0.5千克的菜没有拿走,再把一捆菜放在秤上,指针共转了![]() 那么,后放上的这捆菜有多少千克?
那么,后放上的这捆菜有多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
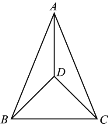
【题目】如图,在△ABC中,AB=AC,D是三角形内一点,连接AD,BD,CD,∠BDC=90°,∠DBC=45°.
(1)求证:∠BAD=∠CAD;
(2)求∠ADB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com