练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
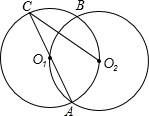
    19．如图，等圆⊙O1和⊙O2相交于A、B两点，⊙O1经过⊙O2的圆心O2，连接AO1，并延长交⊙O1于点C，则∠ACO2的度数为（　　）
    A．60°B．45°C．30°D．20°

    分析 连接O1O2、O2A，根据题意证明△O1O2A是等边三角形，得到∠AO1O2=60°，根据圆周角定理求出∠ACO2的度数．

    解答 解：连接O1O2、O2A，
    由题意得，O1O2=O2A=O1A，
    ∴△O1O2A是等边三角形，
    ∴∠AO1O2=60°，
    ∴∠ACO2=$\frac{1}{2}$∠AO1O2=30°，
    故选：C．

    点评 本题考查的是相交两圆的性质，掌握等边三角形的性质和圆周角定理是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    2．分解因式：2mx-6my=2m（x-3y）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知关于x的一元二次方程（x-1）（x-4）=p2，p为实数．
    （1）求证：方程有两个不相等的实数根；
    （2）p为何值时，方程有整数解．（直接写出三个，不需说明理由）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．如图，两个半径都是4cm的圆外切于点C，一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行，蚂蚁在这8段路径上不断爬行，直到行走2006πcm后才停下来，则蚂蚁停的那一个点为（　　）
    A．D点B．E点C．F点D．G点

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图1，已知抛物线y=ax2-2ax+3（a≠0），与x轴交于A、B两点，与y轴交于点C，若OB=3OA．    
    （1）求抛物线的解析式；    
    （2）连接BC，点P、点Q是第一象限的抛物线上不同的两点，是否存在这样的P点，使得S△BCP＞S△BCQ恒成立？若存在，请求P点的坐标；若不存在，请说明理由；   
    （3）如图2，D为抛物线的顶点在x轴上的正投影，M为线段OC上一点，过点M作直线l交抛物线于E、F两点，连接AE、OE、BF、DF，若△AEO∽△DFB，求M点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，在7×11网格中，已知线段AB和点P，按下列要求画图．
    （1）将线段AB绕点A顺时针旋转90°，得到线段AC，连接BC；
    （2）将△ABC进行平移，使点P在平移后的三角形内．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．在矩形ABCD中，$\frac{AB}{AD}$=a，点G，H分别在边AB，DC上，且HA=HG，点E为AB边上的一个动点，连接HE，把△AHE沿直线HE翻折得到△FHE．如图1，当DH=DA时，
    （1）填空：∠HGA=45度；
    （2）若EF∥HG，求∠AHE的度数，并求此时a的最小值；

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．有一块直角三角形绿地，量得直角边分别为BC=6cm，AC=8cm，现在要将绿地扩充成等腰三角形，且扩充部分是以AC=8cm为直角边的直角三角形，请画出扩充后符合条件的所有等腰三角形（注明相等的边），并直接求出扩充后等腰三角形绿地的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，某校数学兴趣小组为测得大厦AB的高度，在大厦前的平地上选择一点C，测得大厦顶端A的仰角为30°，再向大厦方向前进80米，到达点D处（C、D、B三点在同一直线上），又测得大厦顶端A的仰角为45°，请你计算该大厦的高度．（精确到0.1米，参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）

    查看答案和解析>>

    同步练习册答案