
����Ŀ����֪��![]() ��ֱ��
��ֱ��![]() �����
�����![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ���![]() ���ù�ʽ
���ù�ʽ![]() ���㣮
���㣮
���磺���![]() ��ֱ��
��ֱ��![]() �ľ��룮
�ľ��룮
�⣺��Ϊֱ��![]() ������
������![]() ��
��
���Ե�![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ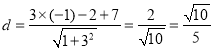 ��
��
�������ϲ��ϣ�����������⣺
��1����![]() ��ֱ��
��ֱ��![]() �ľ��룻
�ľ��룻
��2����֪![]() ��Բ��
��Բ��![]() ������Ϊ
������Ϊ![]() ���뾶
���뾶![]() Ϊ2���ж�
Ϊ2���ж�![]() ��ֱ��
��ֱ��![]() ��λ�ù�ϵ��˵�����ɣ�
��λ�ù�ϵ��˵�����ɣ�
��3����ֱ֪��![]() ��
��![]() ƽ�У�
ƽ�У�![]() ��
��![]() ��ֱ��
��ֱ��![]() �ϵ�������
�ϵ�������![]() ��
��![]() ��ֱ��
��ֱ��![]() ������һ�㣬��
������һ�㣬��![]() �������
�������
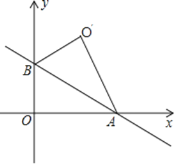
��4����ͼ��ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ���
��ֱ���![]() ��
��![]() ���㣬��
���㣬��![]() ��ֱ��
��ֱ��![]() ���ۺ�õ�
���ۺ�õ�![]() ����
����![]() �ij���
�ij���
���𰸡���1��![]() ����2��
����2��![]() ��ֱ��
��ֱ��![]() ���У����������������3��
�������������������3��![]() ����4��
����4��![]()
��������
��1�����ݵ㵽ֱ�ߵľ��빫ʽ���뼴�ɣ�
��2�����ݵ㵽ֱ�ߵľ��빫ʽ�������Բ��Q��ֱ��![]() �ľ��룬Ȼ�����ֱ����Բ��λ�ù�ϵ�ж����ɣ�
�ľ��룬Ȼ�����ֱ����Բ��λ�ù�ϵ�ж����ɣ�
��3����ֱ��![]() ��ȡһ��
��ȡһ��![]() �����ݵ㵽ֱ�ߵľ��빫ʽ���������Q��ֱ��
�����ݵ㵽ֱ�ߵľ��빫ʽ���������Q��ֱ��![]() �ľ��룬Ȼ�����ƽ����֮��ľ��봦����Ⱥ������������ʽ���㼴�ɣ�
�ľ��룬Ȼ�����ƽ����֮��ľ��봦����Ⱥ������������ʽ���㼴�ɣ�
��4������![]() ��AB�ڵ�
��AB�ڵ�![]() �����۵������ʵã�
�����۵������ʵã�![]() ���Ӷ��ó�ֱ��AB��ֱƽ��
���Ӷ��ó�ֱ��AB��ֱƽ��![]() ���ɵ�OM��AB��
���ɵ�OM��AB��![]() ��Ȼ��㵽ֱ�ߵľ��빫ʽ���������O��ֱ��
��Ȼ��㵽ֱ�ߵľ��빫ʽ���������O��ֱ��![]() �ľ���OM�ij����Ӷ����
�ľ���OM�ij����Ӷ����![]() �ij���
�ij���
�⣺��1�����ݵ㵽ֱ�ߵľ��빫ʽ��֪����![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ���![]() ��
��
��2�����ۣ��ж�![]() ��ֱ��
��ֱ��![]() ���У�
����
���ɣ����ݵ㵽ֱ�ߵľ��빫ʽ��֪����![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ��� ��
��
��![]() �İ뾶Ϊ2��
�İ뾶Ϊ2��
��![]() ��
��
��![]() ��ֱ��
��ֱ��![]() ���У�
����
��3����ֱ��![]() ��ȡһ��
��ȡһ��![]() ��
��
���ݵ㵽ֱ�ߵľ��빫ʽ��֪����![]() ����ֱ��
����ֱ��![]() �ľ���
�ľ���![]() ��
��
��ֱ��![]() ��
��![]() ƽ�У�
ƽ�У�
![]() ��
��
��4���⣺��ͼ������![]() ��AB�ڵ�
��AB�ڵ�![]()
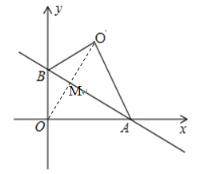
���۵������ʵã�![]() ��
��
��ֱ��AB��ֱƽ��![]()
��OM��AB��![]()
����O��0,0����ֱ��![]() �ľ���OM=
�ľ���OM=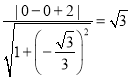
��![]()
��![]() ��
��


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
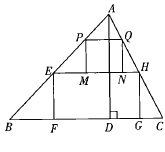
����Ŀ����һ����������ο�ֽ����ABC�����ı�BC=120cm����AD=80cm��Ϊʹ��ֽ���ϵõ�������ã��ְ����ü���һ���ڱ�֮��Ϊ2��5�ľ���ֽƬEFGH��������ֽƬPMNQ���ü�ʱ������ֽƬ�Ľϳ�����BC�ϣ�������ֽƬһ���ھ���ֽƬ�Ľϳ���EH�ϣ����ඥ����ֱ���AB��AC�ϣ�����ü���ʽ��ͼ��ʾ��
��1�������ֽƬ�ϳ���EH�ij���
��2���ü�������ֽƬʱ��С��ͬѧ�ǰ����·������вü��ģ�������ʣ����![]() �����EHƽ�е���λ��һ�������ع�����λ�����˵����EH�����Ĵ�������������ͨ�����㣬�ж�С�ϵļ����Ƿ���ȷ.
�����EHƽ�е���λ��һ�������ع�����λ�����˵����EH�����Ĵ�������������ͨ�����㣬�ж�С�ϵļ����Ƿ���ȷ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
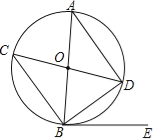
����Ŀ����ͼ������O�У�AB��CD��ֱ����BE�����ߣ�BΪ�е㣬����AD��BC��BD��
��1����֤����ABD�ա�CDB��
��2������DBE=37��������ADC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
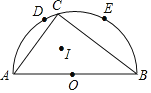
����Ŀ����ͼ����֪��D��E�ǰ�ԲO�ϵ����ȷֵ㣬C�ǻ�DE�ϵ�һ�����㣬����AC��BC����I����ABC�����ģ�����O�İ뾶Ϊ3������C�ӵ�D�˶�����Eʱ����I��֮�˶��γɵ�·������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
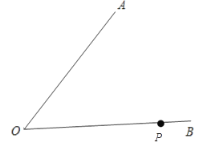
����Ŀ����ͼ![]() ��
��![]() ��������ֱ�Ĺ�·����
��������ֱ�Ĺ�·����![]() ��
��![]() �ϵ�һ�����У������뽨һ��������
�ϵ�һ�����У������뽨һ��������![]() ��Ҫ��������·�ľ�����ȣ��ҷ�����������
��Ҫ��������·�ľ�����ȣ��ҷ�����������![]() �ľ�����������������������
�ľ�����������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��֯ѧ�����̳��μ����ʵ��������Dz�����ij��Ʒ���˶�Ь�����۹�������֪���˶�Ьÿ˫�Ľ���Ϊ120Ԫ��ΪѰ����ʵ����ۼ۸������4���������������������ʾ��

��1���۲�������ݣ�x��y����ʲô������ϵ����������������ϵʽ��
��2�����̳��ƻ�ÿ�����������Ϊ3000Ԫ�����䵥��Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������һ��ǽ��ǽ�ij��Ȳ�����45m������80m�������Χһ�����γ��أ�

��1������Χ����ʹ���γ��ص����Ϊ750m2��
��2���ܷ�ʹ��Χ���γ��ص����Ϊ810m2��Ϊʲô��
��3������Χ����ʹΧ���ľ��γ���������������Ϊ���٣���ͨ������˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c��a��0����һ�κ���y��ax+c��ͬһ����ϵ�е�ͼ�����Ϊ���� ����
A. B.
B.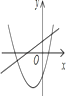 C.
C.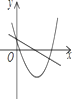 D.
D.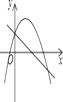
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�涨max��a��b����![]() �����磺max����1��2����2��max��3��3����3��
�����磺max����1��2����2��max��3��3����3��
��֪����֪����y��max��x+1����2x+4��
��1����x��3ʱ��y��_____��
��2����y��3ʱ��x��______��
��3����y��x�����������ʱ��x��ȡֵ��ΧΪ______��
��4������1��x��4ʱ��y��ȡֵ��ΧΪ______��
̽������֪����y��max��x+2��![]() ����ֱ��y��m��mΪ�������뺯��y��max��x+2��
����ֱ��y��m��mΪ�������뺯��y��max��x+2��![]() ������6��x��3����ͼ��������������ʱ��m��ȡֵ��ΧΪ_______��
������6��x��3����ͼ��������������ʱ��m��ȡֵ��ΧΪ_______��
��չ����֪����y��max����x2+2nx����nx����nΪ������n��0������![]() n��3��x��2ʱ������x��������ֵy�ȼ�С������ֱ��д��n��ȡֵ��Χ��
n��3��x��2ʱ������x��������ֵy�ȼ�С������ֱ��д��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com