
 (1)请在横线上填写合适的内容,完成下面的证明:
(1)请在横线上填写合适的内容,完成下面的证明:分析 (1)根据平行线的性质可得;
(2)过点P作PM∥AB,过点Q作QN∥CD,将∠A、∠P、∠Q、∠C划分为6个3对同旁内角,由平行线的性质可得;
(3)延长PQ交CD于点E,延长QP交AB于点F,可得∠BFP=∠CEQ,根据三角形外角定理知∠BFP=∠BPQ-∠B、∠CEQ=∠PQC-∠C,整理后即可得.
解答 解:(1)过P作PM∥AB,
所以∠A=∠APM,(两直线平行,内错角相等)
因为 PM∥AB,AB∥CD (已知 )
所以 PM∥CD,
所以∠C=∠CPM,(两直线平行,内错角相等)
因为∠APC=∠APM+∠CPM
所以∠APC=∠A+∠C (等量代换 ),
故答案为:两直线平行,内错角相等;∠CPM;两直线平行,内错角相等.
(2)如图②,过点P作PM∥AB,过点Q作QN∥CD,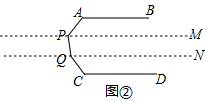
∴∠A+∠APM=180°,∠C+∠CQN=180°,
又∵AB∥CD,
∴PM∥QN,
∴∠MPQ+∠NQP=180°,
则∠A+∠APQ+∠CQP+∠C=∠A+∠APM+∠MPQ+∠NQP+∠CQN+∠C=540°,
故答案为:540°.
(3)如图③,延长PQ交CD于点E,延长QP交AB于点F,
∵AB∥CD,
∴∠BFP=∠CEQ,
又∵∠BPQ=∠BFP+∠B,∠PQC=∠CEQ+∠C,
即∠BFP=∠BPQ-∠B,∠CEQ=∠PQC-∠C,
∴∠BPQ-∠B=∠PQC-∠C,即y-x=z-m,
∴m=x-y+z,
故答案为:x-y+z.
点评 本题主要考查平行线的性质,作出合适的辅助线将待求角恰当分割是解题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
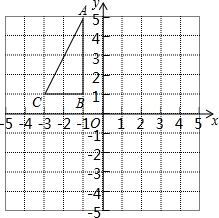 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,5),B(-1,1),C(-3,1).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,5),B(-1,1),C(-3,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
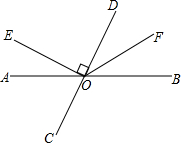 如图,直线AB、CD相交于点O,OE⊥CD,OF平分∠BOD.
如图,直线AB、CD相交于点O,OE⊥CD,OF平分∠BOD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com