
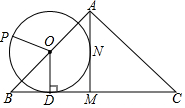
 如图,在△ABC中,AB=AC,点O为边AB的中点,OD⊥BC于点D,AM⊥BC于点M,以点O为圆心,线段OD为半径的圆与AM相切于点N.
如图,在△ABC中,AB=AC,点O为边AB的中点,OD⊥BC于点D,AM⊥BC于点M,以点O为圆心,线段OD为半径的圆与AM相切于点N.分析 (1)如图1中,连接ON.只要证明四边形ODMN是正方形即可解决问题.
(2)①如图2中,连接OC、PC.由PC≤OC+OP,推出当点P在CO的延长线时,P、O、C共线时,PC的值最大,最大值为OC+OP.
②当OB为对角线时,OP∥BD,可得∠BOP=∠ABC=45°,当OB为边时,OP′∥BC,可得∠BOP′=180°-∠ABC=135°.
解答 (1)证明:如图1中,连接ON.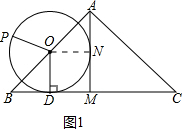
∵AM是⊙O的切线,
∴ON⊥AM,
∵OD⊥BC,AM⊥BC,
∴∠ODM=∠ONM=∠DMN=90°,
∴四边形ODMN是矩形,
∵OD=ON,
∴四边形ODMN是正方形,
∴OD=ON=DM=MN,
∵OA=OB,OD∥AM,ON∥BM,
∴BD=DM,AN=MN,
∴BD=AN;
(2)①如图2中,连接OC、PC.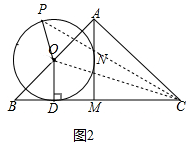
∵PC≤OC+OP,
∴当点P在CO的延长线时,P、O、C共线时,PC的值最大,最大值为OC+OP.
由(1)可知,BM=AM,∠AMB=90°,
∴∠B=45°,
∵AB=AC=4,
∴△ABC是等腰直角三角形,BM=AM=MC=2$\sqrt{2}$,OP=OD=BD=DM=$\sqrt{2}$,
∴OA=2,OC=$\sqrt{O{A}^{2}+A{C}^{2}}$=2$\sqrt{5}$,
∴PC的最大值为2$\sqrt{5}$+$\sqrt{2}$;
②如图3中,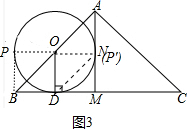
由题意以O,D,B,P为顶点四边形是平行四边形
当OB为对角线时,OP∥BD,可得∠BOP=∠ABC=45°,
当OB为边时,OP′∥BC,可得∠BOP′=180°-∠ABC=135°.
综上所述,当∠POB=45°或135°时,以O,D,B,P为顶点四边形是平行四边形;
点评 本题考查圆综合题、切线的性质、正方形的判定和性质、等腰直角三角形的判定和性质、平行四边形的判定和性质、三角形三边关系等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,本题的突破点是证明四边形ODMN是正方形,属于中考压轴题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
 甲乙两台智能机器人从同一地点P出发,沿着笔直的路线行走了450cm到点Q.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.甲匀速走完全程.两机器人行走的路程y(cm)与时间x(s)之间的函数图象如图所示.根据图象所提供的信息解答下列问题:
甲乙两台智能机器人从同一地点P出发,沿着笔直的路线行走了450cm到点Q.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.甲匀速走完全程.两机器人行走的路程y(cm)与时间x(s)之间的函数图象如图所示.根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
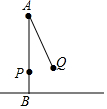 如图,旗杆AB顶端系一根绳子AP,绳子底端离地面的距离为1m,小明将绳子拉到AQ的位置,测得∠PAQ=25°,此时点Q离地面的高度为1.5m,求旗杆的高度(结果保留整数.sin25°=0.42,cos25°=0.90,tan25°=0.47)
如图,旗杆AB顶端系一根绳子AP,绳子底端离地面的距离为1m,小明将绳子拉到AQ的位置,测得∠PAQ=25°,此时点Q离地面的高度为1.5m,求旗杆的高度(结果保留整数.sin25°=0.42,cos25°=0.90,tan25°=0.47)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
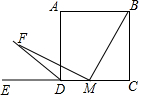 如图,在正方形ABCD中,AB=2,点M为正方形ABCD的边CD上的动点(与点C,D不重合),连接BM,作MF⊥BM,与正方形ABCD的外角∠ADE的平分线交于点F.设CM=x,△DFM的面积为y,则y与x之间的函数关系式y=-$\frac{1}{2}$x2+x.
如图,在正方形ABCD中,AB=2,点M为正方形ABCD的边CD上的动点(与点C,D不重合),连接BM,作MF⊥BM,与正方形ABCD的外角∠ADE的平分线交于点F.设CM=x,△DFM的面积为y,则y与x之间的函数关系式y=-$\frac{1}{2}$x2+x.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
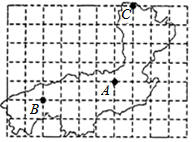 如图是某植物园的平面图,图中A馆所在地用坐标表示为(1,0),B馆所在地用坐标表示为(-3,-1),那么C馆所在地用坐标表示为(2,4).
如图是某植物园的平面图,图中A馆所在地用坐标表示为(1,0),B馆所在地用坐标表示为(-3,-1),那么C馆所在地用坐标表示为(2,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com