
 如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.分析 (1)由同圆半径相等和对顶角相等得∠OBP=∠APC,由圆的切线性质和垂直得∠ABP+∠OBP=90°和∠ACB+∠APC=90°,则∠ABP=∠ACB,根据等角对等边得AB=AC;
(2)设⊙O的半径为r,分别在Rt△AOB和Rt△ACP中根据勾股定理列等式,并根据AB=AC得52-r2=(2$\sqrt{5}$)2-(5-r)2,求出r的值即可.
解答 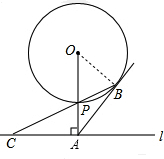 证明:(1)连接OB,
证明:(1)连接OB,
∵OB=OP,
∴∠OPB=∠OBP,
∵∠OPB=∠APC,
∴∠OBP=∠APC,
∵AB与⊙O相切于点B,
∴OB⊥AB,
∴∠ABO=90°,
∴∠ABP+∠OBP=90°,
∵OA⊥AC,
∴∠OAC=90°,
∴∠ACB+∠APC=90°,
∴∠ABP=∠ACB,
∴AB=AC;
(2)设⊙O的半径为r,
在Rt△AOB中,AB2=OA2-OB2=52-r2,
在Rt△ACP中,AC2=PC2-PA2,
AC2=(2$\sqrt{5}$)2-(5-r)2,
∵AB=AC,
∴52-r2=(2$\sqrt{5}$)2-(5-r)2,
解得:r=3,
则⊙O的半径为3.
点评 本题考查了圆的切线的性质,圆的切线垂直于经过切点的半径;并利用勾股定理列等式,求圆的半径;此类题的一般做法是:若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系;简记作:见切点,连半径,见垂直.


科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠C=Rt∠,AB=5,AC=4,则sinA的值是( )
如图,在△ABC中,∠C=Rt∠,AB=5,AC=4,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:初中数学 来源:2017届江苏省宜兴市宜城环科园教学联盟九年级下学期第一次质量检测数学试卷(解析版) 题型:判断题
如图,在矩形ABCD中,AB=3,BC=4.动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点后立刻以原来的速度沿AB返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点C时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t >0)秒.
(1)在点Q从B到A的运动过程中,
①当t= 时,PQ⊥AC;
②求△APQ的面积S关于t的函数关系式,并写出t的取值范围;
(2)伴随着P、Q两点的运动,线段PQ的垂直平分线为l.
①当l经过点A时,射线QP交AD于点E,求AE的长;
②当l经过点B时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-$\frac{1}{2}$x2-x-$\frac{3}{2}$ | B. | y=-$\frac{1}{2}$x2+x-$\frac{1}{2}$ | C. | y=-$\frac{1}{2}$x2+x-$\frac{3}{2}$ | D. | y=-$\frac{1}{2}$x2-x-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2x2y•3xy2=-6x2y2 | B. | (-x-2y)(x+2y)=x2-4y2 | ||
| C. | 6x3y2÷2x2y=3xy | D. | (4x3y2)2=16x9y4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com