
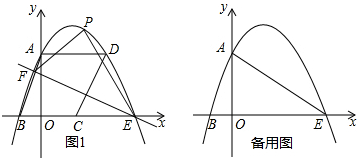
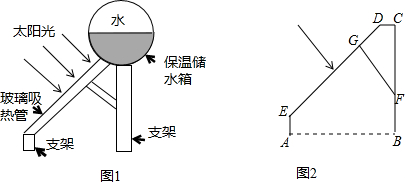
���� ��1����A��B��C��������꣬���ô���ϵ��������������߽���ʽ��
��2����A��C��������ƽ���ı��ε����ĵ����꣬�������ߵĶԳ��Կ����E�����꣬�Ӷ������ֱ��EF�Ľ���ʽ����PH��x�ᣬ��ֱ��l�ڵ�M����FN��PH�������t��ʾ��PM�ij����Ӷ��ɱ�ʾ����PEF������������ö��κ��������ʿ���������ֵ�����������ֵ�����������ɣ�
��3���������֪�С�PAE=90����APE=90���������������PAE=90��ʱ����PG��y�ᣬ���õ���ֱ�������ε����ʿɵõ�����t�ķ��̣������t��ֵ������APE=90��ʱ����PK��x�ᣬAQ��PK�����֤�á�PKE�ס�AQP���������������ε����ʿɵõ�����t�ķ��̣������t��ֵ��
��� �⣺
��1��������ɵ�$\left\{\begin{array}{l}{c=3}\\{a-b+c=0}\\{4a+2b+c=3}\end{array}\right.$�����$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$��
�������߽���ʽΪy=-x2+2x+3��
��2����A��0��3����D��2��3����
��BC=AD=2��
��B��-1��0����
��C��1��0����
���߶�AC���е�Ϊ��$\frac{1}{2}$��$\frac{3}{2}$����
��ֱ��l��ƽ���ı���ABCD�ָ�Ϊ�����������֣�
��ֱ��l��ƽ���ı��εĶԳ����ģ�
��A��D���ڶԳ���Գƣ�
�������߶Գ���Ϊx=1��
��E��3��0����
��ֱ��l�Ľ���ʽΪy=kx+m����E��ͶԳ������������ɵ�$\left\{\begin{array}{l}{\frac{1}{2}k+m=\frac{3}{2}}\\{3k+m=0}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{3}{5}}\\{m=\frac{9}{5}}\end{array}\right.$��
��ֱ��l�Ľ���ʽΪy=-$\frac{3}{5}$x+$\frac{9}{5}$��
����ֱ��l�������߽���ʽ�ɵ�$\left\{\begin{array}{l}{y=-\frac{3}{5}x+\frac{9}{5}}\\{y=-{x}^{2}+2x+3}\end{array}\right.$�����$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=-\frac{2}{5}}\\{y=\frac{51}{25}}\end{array}\right.$��
��F��-$\frac{2}{5}$��$\frac{51}{25}$����
��ͼ1����PH��x�ᣬ��l�ڵ�M����FN��PH��
��P�������Ϊt��
��P��t��-t2+2t+3����M��t��-$\frac{3}{5}$t+$\frac{9}{5}$����
��PM=-t2+2t+3-��-$\frac{3}{5}$t+$\frac{9}{5}$��=-t2+$\frac{13}{5}$t+$\frac{6}{5}$��
��S��PEF=S��PFM+S��PEM=$\frac{1}{2}$PM•FN+$\frac{1}{2}$PM•EH=$\frac{1}{2}$PM•��FN+EH��=$\frac{1}{2}$��-t2+$\frac{13}{5}$t+$\frac{6}{5}$����3+$\frac{2}{5}$��=-$\frac{17}{10}$��t-$\frac{13}{10}$��+$\frac{289}{100}$��$\frac{17}{10}$��
�൱t=$\frac{13}{10}$ʱ����PEF�������������ֵΪ$\frac{289}{100}$��$\frac{17}{10}$��
�����ֵ��������Ϊ$\root{3}{\frac{289}{100}��\frac{17}{10}}$=$\frac{17}{10}$��
��3����ͼ��֪��PEA��90�㣬
��ֻ���С�PAE=90����APE=90�㣬
�ٵ���PAE=90��ʱ����ͼ2����PG��y�ᣬ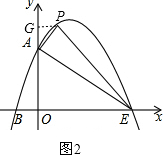
��OA=OE��
���OAE=��OEA=45�㣬
���PAG=��APG=45�㣬
��PG=AG��
��t=-t2+2t+3-3����-t2+t=0�����t=1��t=0����ȥ����
�ڵ���APE=90��ʱ����ͼ3����PK��x�ᣬAQ��PK��
��PK=-t2+2t+3��AQ=t��KE=3-t��PQ=-t2+2t+3-3=-t2+2t��
�ߡ�APQ+��KPE=��APQ+��PAQ=90�㣬
���PAQ=��KPE���ҡ�PKE=��PQA��
���PKE�ס�AQP��
��$\frac{PK}{AQ}$=$\frac{KE}{PQ}$����$\frac{-{t}^{2}+2t+3}{t}$=$\frac{3-t}{-{t}^{2}+2t}$����t2-t-1=0�����t=$\frac{1+\sqrt{5}}{2}$��t=$\frac{1-\sqrt{5}}{2}$��-$\frac{5}{2}$����ȥ����
���Ͽ�֪�������������ĵ�P��t��ֵΪ1��$\frac{1+\sqrt{5}}{2}$��
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ������ƽ���ı��ε����ʡ����κ��������ʡ������ε������ֱ�������ε����ʡ����������ε��ж������ʡ�����˼�뼰��������˼���֪ʶ���ڣ�1����ע�����ϵ��ʾ��Ӧ�ã��ڣ�2������t��ʾ����PEF������ǽ���Ĺؼ����ڣ�3���з�����������ֱ����õ���ֱ�������κ����������ε����ʵõ�����t�ķ����ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���������ϴ��ѶȽϴ�


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
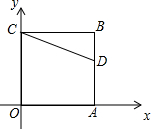 ��ͼ��������OABC������OA��OC�ֱ���x���ϣ���D��5��3���ڱ�AB�ϣ���CΪ���ģ��ѡ�CDB�Ƶ�C˳ʱ����ת90�㣬����ת���D�Ķ�Ӧ��D��������ǣ�-2��0����
��ͼ��������OABC������OA��OC�ֱ���x���ϣ���D��5��3���ڱ�AB�ϣ���CΪ���ģ��ѡ�CDB�Ƶ�C˳ʱ����ת90�㣬����ת���D�Ķ�Ӧ��D��������ǣ�-2��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
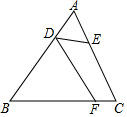 ��ͼ���ڡ�ABC�У�AB��AC��D��E�ֱ�Ϊ��AB��AC�ϵĵ㣮AC=3AD��AB=3AE����FΪBC����һ�㣬����һ��������DF��AC�����BFD=��A������ʹ�á�FDB���ADE���ƣ���ֻ��д��һ����
��ͼ���ڡ�ABC�У�AB��AC��D��E�ֱ�Ϊ��AB��AC�ϵĵ㣮AC=3AD��AB=3AE����FΪBC����һ�㣬����һ��������DF��AC�����BFD=��A������ʹ�á�FDB���ADE���ƣ���ֻ��д��һ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
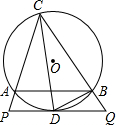 ��ͼ����ABC�ڽ��ڡ�O��CDƽ�֡�ACB����O��D������D��PQ��AB�ֱ�CA��CB�ӳ�����P��Q������BD��
��ͼ����ABC�ڽ��ڡ�O��CDƽ�֡�ACB����O��D������D��PQ��AB�ֱ�CA��CB�ӳ�����P��Q������BD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
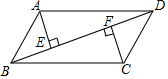 ��֪����ͼ����ƽ���ı���ABCD�У�AE��BD��CF��BD������ֱ�ΪE��F����֤����ADE�ա�CBF��
��֪����ͼ����ƽ���ı���ABCD�У�AE��BD��CF��BD������ֱ�ΪE��F����֤����ADE�ա�CBF���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com