
【题目】如图,四边形ABCD是平行四边形,AD与圆相切,请在下图中,仅用无刻度的直尺按要求画图.
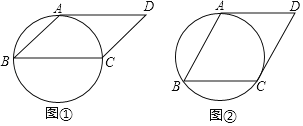
(1)若BC是圆的直径,画出平行四边形ABCD的边CD上的高;
(2)若CD与圆相切,画出平行四边形ABCD的边BC上的高AE.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)连接AC,根据圆周角定理可得∠BAC=90°,则AC⊥AB,由平行四边形的性质可得AB∥CD,继而可得AC即为平行四边形ABCD的边CD上的高;
(2)连接BD交圆于点E,连接CE并延长交AD于点F,则CF⊥BC,过点A作AE∥CF,根据切线性质可得AD=CD,继而得四边形ABCD是菱形,根据菱形的性质可得BD⊥AC,BD平分AC,根据垂径定理证得:BE为圆的直径,进而可得CF⊥BC,继而有AE⊥BC, 即AE是平行四边形ABCD的边BC上的高.
解:(1)如图①所示,连接AC,AC为所求的高;
理由如下:∵BC是圆的直径,
∴∠BAC=90°
∴AC⊥AB,
∵四边形ABCD是平行四边形,
∴AB∥CD
∴AC⊥CD
∴AC是平行四边形ABCD的边CD上的高;

(2)如图②所示,连接BD交圆于点E,连接CE并延长交AD于点F,则CF⊥AD,过点A作AE∥CF,则AE即为所求的高.
理由如下:∵AD、CD都与圆相切
∴AD=CD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形,
∴BD⊥AC,BD平分AC
∴BE是圆的直径,
∴∠BCE=90°
∴CF⊥BC
又∵AE∥CF
∴AE⊥BC,即AE是平行四边形ABCD的边BC上的高。



 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
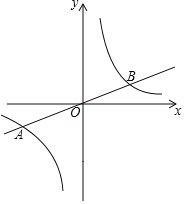
【题目】如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点.
两点.![]() 是第一象限内反比例函数图象上一点,过点
是第一象限内反比例函数图象上一点,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 的面积为
的面积为![]() ,则点
,则点![]() 的坐标为_____________.
的坐标为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
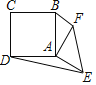
【题目】如图,正方形ABCD和Rt△AEF,AB=5,AE=AF=4,连接BF,DE.若△AEF绕点A旋转,当∠ABF最大时,S△ADE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且![]() ,过点C的直线CD
,过点C的直线CD![]() BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
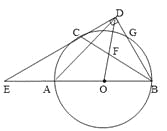
(1)求证:CD是⊙O的切线.
(2)若![]() ,求
,求![]() E的度数.
E的度数.
(3)连接AD,在(2)的条件下,若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+3x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=4.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=4:3时,求点D的坐标.
(3)如图2,点E的坐标为(0,-2),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.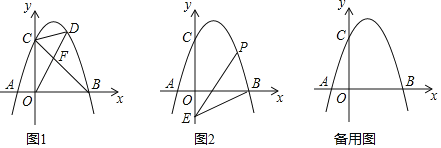
查看答案和解析>>
科目:初中数学 来源: 题型:
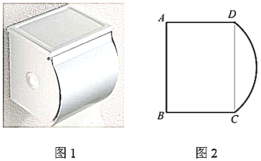
【题目】如图1是一种纸巾盒,由盒身和圆弧盖组成,通过圆弧盖的旋转来开关纸巾盒.如图2是其侧面简化示意图,已知矩形![]() 的长
的长![]() ,宽
,宽![]() ,圆弧盖板侧面
,圆弧盖板侧面![]() 所在圆的圆心
所在圆的圆心![]() 是矩形
是矩形![]() 的中心,绕点
的中心,绕点![]() 旋转开关(所有结果保留小数点后一位).
旋转开关(所有结果保留小数点后一位).
(1)求![]() 所在
所在![]() 的半径长及
的半径长及![]() 所对的圆心角度数;
所对的圆心角度数;
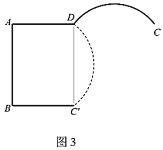
(2)如图3,当圆弧盖板侧面![]() 从起始位置
从起始位置![]() 绕点
绕点![]() 旋转
旋转![]() 时,求
时,求![]() 在这个旋转过程中扫过的的面积.
在这个旋转过程中扫过的的面积.
参考数据:![]() ,
,![]() ,
,![]() 取3.14.
取3.14.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,作
,作![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作圆.
为半径作圆.
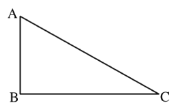
(1)依据题意补充完整图形;(尺规作图,保留作图痕迹,不写作法)
(2)求证:![]() 与直线
与直线![]() 相切;
相切;
(3)在(2)的条件下,若![]() 与直线
与直线![]() 相切的切点为
相切的切点为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,![]() ;其中
;其中![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,(为坐标原点,点![]() ,点
,点![]() 是
是![]() 中点,连接(
中点,连接(![]() 将
将![]() 绕点
绕点![]() 顺时针旋转,得到
顺时针旋转,得到![]() ,记旋转角为
,记旋转角为![]() ,点
,点![]() 的对应点分别是
的对应点分别是![]() ,连接
,连接![]() 是
是![]() 中点,连接
中点,连接![]() .
.
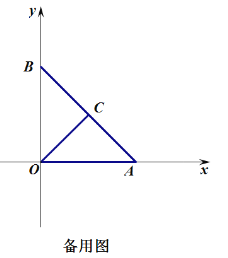
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;

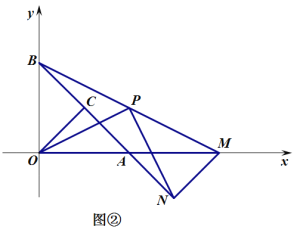
(2)如图②,当![]() 时,求证
时,求证![]() ,且
,且![]() ;
;
(3)当![]() 旋转至点
旋转至点![]() 共线时,求点
共线时,求点![]() 的坐标(直接写出结果即可) .
的坐标(直接写出结果即可) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为改善办学条件,计划采购A、B两种型号的空调,已知采购3台A型空调和2台B型空调,需费用39000元;4台A型空调比5台B型空调的费用多6000元.
(1)求A型空调和B型空调每台各需多少元;
(2)若学校计划采购A、B两种型号空调共30台,且A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com