
【题目】如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=![]() CD,求证:∠AEF=90°.
CD,求证:∠AEF=90°.

科目:初中数学 来源: 题型:
【题目】【问题提出】如图①,已知海岛A到海岸公路BD的距离为AB,C为公路BD上的酒店,从海岛A到酒店C,先乘船到登陆点D,船速为a,再乘汽车,车速为船速的n倍,点D选在何处时,所用时间最短?
【特例分析】若n=2,则时间t= ![]() +
+ ![]() ,当a为定值时,问题转化为:在BC上确定一点D,使得AD+
,当a为定值时,问题转化为:在BC上确定一点D,使得AD+ ![]() 的值最小.如图②,过点C做射线CM,使得∠BCM=30°.
的值最小.如图②,过点C做射线CM,使得∠BCM=30°.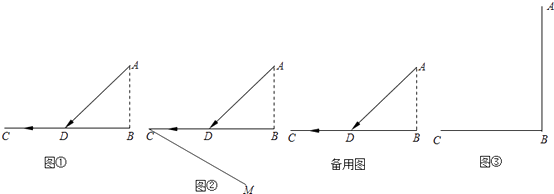
(1)过点D作DE⊥CM,垂足为E,试说明:DE= ![]() ;
;
(2)【问题解决】请在图②中画出所用时间最短的登陆点D′,并说明理由.
(3)【模型运用】请你仿照“特例分析”中的相关步骤,解决图①中的问题(写出具体方案,如相关图形呈现、图形中角所满足的条件、作图的方法等).
(4)如图③,海面上一标志A到海岸BC的距离AB=300m,BC=300m.救生员在C点处发现标志A处有人求救,
立刻前去营救,若救生员在岸上跑的速度都是6m/s,在海中游泳的速度都是2m/s,求救生员从C点出发到
达A处的最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.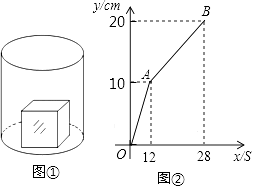
(1)正方体的棱长为cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(﹣4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y= ![]() (k>0,x>0)的图象经过点C,则k的值为( )
(k>0,x>0)的图象经过点C,则k的值为( )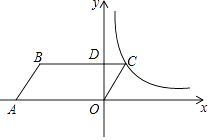
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.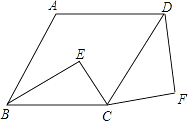
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,(1)∠AOB=60°,∠BOC=36°OD平分∠BOC,OE平分∠AOC,则∠EOD=____度;
(2)若∠AOB=90°,OD平分∠BOC,OE平分∠AOC,则∠EOD=__________;
(3)若∠AOB=α,其它条件同(2),则∠EOD=_________________.
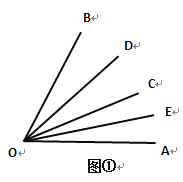
类比应用:
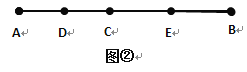
如图②,已知线段AB,C是线段AB上任一点,D、E分别是AC、CB的中点,试猜想DE与AB的数量关系为_____________,并写出求解过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com