
 如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,求∠BAD的度数.
如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,求∠BAD的度数.  小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:单选题
九(2)班体育委员用划记法统计本班40名同学投掷实心球的成绩,结果如图所示:则这40名同学投掷实心球的成绩的众数和中位数分别是( )
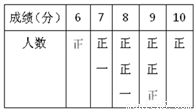
A. 8,8 B. 8,8.5 C. 9,8 D. 9,8.5
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
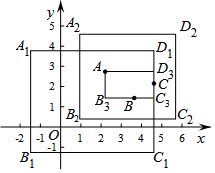
 如图,在平面直角坐标系xOy中,?OABC的边OC在x轴上,A(1,4)、C(3,0)点D在AB上,D(3,4),过点D的直线l平分?OABC的面积,现将l绕点A逆时针旋转90°得直线l′,则直线l′的函数解析式为( )
如图,在平面直角坐标系xOy中,?OABC的边OC在x轴上,A(1,4)、C(3,0)点D在AB上,D(3,4),过点D的直线l平分?OABC的面积,现将l绕点A逆时针旋转90°得直线l′,则直线l′的函数解析式为( )| A. | y=-2x+6 | B. | y=-2x+6.5 | C. | $y=-\frac{1}{2}x+\frac{5}{2}$ | D. | $y=-\frac{1}{2}x+\frac{13}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com