
【题目】如图,⊙O过点B、C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( ) 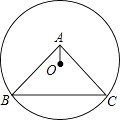
A.6
B.13
C.![]()
D.2 ![]()
【答案】C
【解析】解:过O作OD⊥BC, ∵BC是⊙O的一条弦,且BC=6,
∴BD=CD= ![]() BC=
BC= ![]() ×6=3,
×6=3,
∴OD垂直平分BC,又AB=AC,
∴点A在BC的垂直平分线上,即A,O、D三点共线,
∵△ABC是等腰直角三角形,
∴∠ABC=45°,
∴△ABD也是等腰直角三角形,
∴AD=BD=3,
∵OA=1,
∴OD=AD﹣OA=3﹣1=2,
在Rt△OBD中,
OB= ![]() =
= ![]() =
= ![]()
故选C.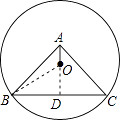
过O作OD⊥BC,由垂径定理可知BD=CD= ![]() BC,根据△ABC是等腰直角三角形可知∠ABC=45°,故△ABD也是等腰直角三角形,BD=AD,再由OA=1可求出OD的长,在Rt△OBD中利用勾股定理即可求出OB的长.
BC,根据△ABC是等腰直角三角形可知∠ABC=45°,故△ABD也是等腰直角三角形,BD=AD,再由OA=1可求出OD的长,在Rt△OBD中利用勾股定理即可求出OB的长.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案科目:初中数学 来源: 题型:
【题目】一个袋子中装有3个红球和2个黄球,这些球的形状、大小.质地完全相同,在看不到球的条件下,随机从袋子里同时摸出2个球,其中2个球的颜色相同的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4米. 
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:(1)(2)的计算结果精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,
≈1.73, ![]() ≈2.24,
≈2.24, ![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,平行四边形ABCD在第一象限,且AB∥x轴,直线y=﹣x从原点出发沿x轴正方向平移,被平行四边形ABCD截得的线段EF的长度l与平移的距离m的函数图象如图②,那么平行四边形ABCD的面积为( )
A.4
B.![]()
C.8
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司经销甲种型号电脑,今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑.已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,C是AB延长线上一点,BC=OB,CE是⊙O的切线,切点为D,过点A作AE⊥CE,垂足为E,则CD:DE的值是( ) 
A.![]()
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com