
【题目】如图,△AOB中,A(-8,0),B(0,![]() ),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴交于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F.
),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴交于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F.
(1)求证:EF为⊙P的切线;
(2)求⊙P的半径.
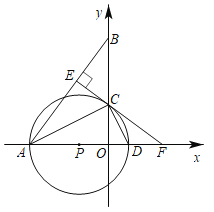
【答案】(1)详见解析;(2)5
【解析】
(1)连接CP,根据等腰三角形的性质得到∠PAC=∠PCA,由角平分线的定义得到∠PAC=∠EAC,等量代换得到∠PCA=∠EAC,推出PC∥AE,于是得到结论;
(2)根据角平分线的定义得到∠BAC=∠OAC,根据等腰三角形的性质得到∠PCA=∠PAC,等量代换得到∠BAC=∠ACP,推出PC∥AB,根据相似三角形的性质即可得到结论.
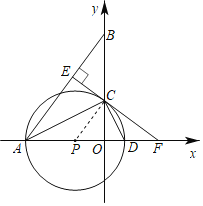
(1)证明:连接CP, ∵AP=CP,
∴∠PAC=∠PCA,
∵AC平分∠OAB,
∴∠PAC=∠EAC,
∴∠PCA=∠EAC,
∴PC∥AE,
∵CE⊥AB,
∴CP⊥EF,
即EF是⊙P的切线;
(2)由(1)知,PC∥AB,
∴△OPC∽△OAB,
∴ ![]()
∵A(-8,0),B(0,![]() ),
),
∴OA=8,OB=![]() ,
,
∴AB=![]()
![]() ,
,
∴ 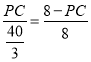 ,
,
∴PC=5,
∴⊙P的半径为5.


科目:初中数学 来源: 题型:
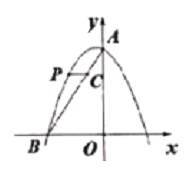
【题目】如图,二次函数y=-x2+(n-1)x+3的图像与y轴交于点A,与x轴的负半轴交于点B(-2,0)
(1)求二次函数的解析式;
(2)点P是这个二次函数图像在第二象限内的一线,过点P作y轴的垂线与线段AB交于点C,求线段PC长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“脐橙结硕果,香飘引客来”,赣南脐橙以其“外表光洁美观,肉质脆嫩,风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售,若用2辆A型车和1辆B型车载满脐橙一次可运走10吨;用1辆A型车和2辆B型车载满脐橙一次可运走11吨.现有脐橙31吨,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满脐橙.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满脐橙一次可分别运送多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若1辆A型车需租金100元/次,1辆B型车需租金120元/次.请选出费用最少的租车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
正方形内“奇妙点”及性质探究
定义:如图1,在正方形![]() 中,以
中,以![]() 为直径作半圆
为直径作半圆![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,与半圆
,与半圆![]() 交于点
交于点![]() .我们称点
.我们称点![]() 为正方形
为正方形![]() 的一个“奇妙点”.过奇妙点的多条线段与正方形
的一个“奇妙点”.过奇妙点的多条线段与正方形![]() 无论是位置关系还是数量关系,都具有不少优美的性质值得探究.
无论是位置关系还是数量关系,都具有不少优美的性质值得探究.
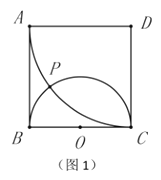
性质探究:如图2,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,则
,则![]() 为半圆
为半圆![]() 的切线.
的切线.
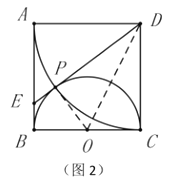
证明:连接![]() .
.
由作图可知,![]() ,
,
又![]() .
.
![]()
![]() ,∴
,∴![]() 是半圆
是半圆![]() 的切线.
的切线.
问题解决:
(1)如图3,在图2的基础上,连接![]() .请判断
.请判断![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
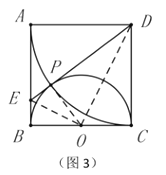
(2)在(1)的条件下,请直接写出线段![]() 之间的数量关系;
之间的数量关系;
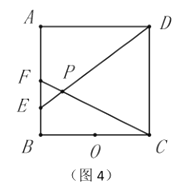
(3)如图4,已知点![]() 为正方形
为正方形![]() 的一个“奇妙点”,点
的一个“奇妙点”,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,请写出
,请写出![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
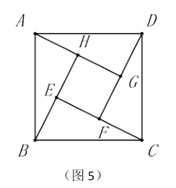
(4)如图5,已知点![]() 为正方形
为正方形![]() 的四个“奇妙点”.连接
的四个“奇妙点”.连接![]() ,恰好得到一个特殊的“赵爽弦图”.请根据图形,探究并直接写出一个不全等的几何图形面积之间的数量关系.
,恰好得到一个特殊的“赵爽弦图”.请根据图形,探究并直接写出一个不全等的几何图形面积之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象分别位于第二、第四象限,
的图象分别位于第二、第四象限,![]() 、
、![]() 两点在该图象上,下列命题:①过点
两点在该图象上,下列命题:①过点![]() 作
作![]() 轴,
轴,![]() 为垂足,连接
为垂足,连接![]() .若
.若![]() 的面积为3,则
的面积为3,则![]() ;②若
;②若![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() 其中真命题个数是( )
其中真命题个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 为
为![]() 中点,以
中点,以![]() 为边作正方形
为边作正方形![]() ,边
,边![]() 交
交![]() 于点
于点![]() .在边
.在边![]() 上取点
上取点![]() 使
使![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
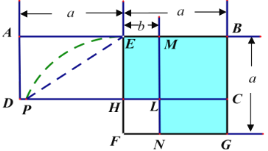
(1)请你利用该图解释平方差公式:![]() .
.
(2)现以点![]() 为圆心,
为圆心,![]() 为半径作圆弧交线段
为半径作圆弧交线段![]() 于点
于点![]() ,连接
,连接![]() .若点
.若点![]() 在同一直线上,求
在同一直线上,求![]() 的值?
的值?
(3)记![]() 的面积为
的面积为![]() ,图中四边形
,图中四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某学校为了了解九年级学生的体能情况,抽取了部分学生进行了体能测试,学生的测试成绩分四类:A:优秀;B:良好;C:合格;D不合格,将抽测学生的成绩绘制成如下两幅不完整的统计图,请根据统计图解答下列问题:
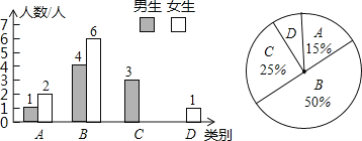
(1)求本次调查的学生总人数;
(2)成绩为C的女生有______人,成绩为D的男生有______人;
(3)扇形统计图中成绩为D的学生所对应的扇形的圆心角度数为______;
(4)补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
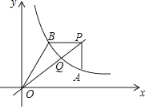
【题目】如图,直线y=mx与反比例函数![]() (x>0)的图象交于Q点,点B(3,4)在反比例函数
(x>0)的图象交于Q点,点B(3,4)在反比例函数![]() 的图象上,过点B作PB∥x轴交OQ于点P,过点P作PA∥y轴交反比例函数图象于点A.
的图象上,过点B作PB∥x轴交OQ于点P,过点P作PA∥y轴交反比例函数图象于点A.
(1)若点A的纵坐标为![]() ,求反比例函数及直线OP的解析式;
,求反比例函数及直线OP的解析式;
(2)连接OB,在(1)的条件下,求sin∠BOP的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com