
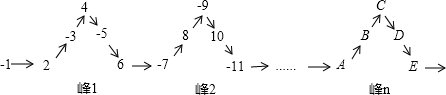
分析 观察不难发现,每5个数为一个循环组依次循环,表示出“峰n”中峰顶C的位置的数的绝对值,然后把n=202代入计算,结果为奇数则是负数,结果为偶数是正数;再表示出“峰2n+1”中峰顶C上的数的绝对值,然后减去1得到B位置上的数的绝对值,结果为奇数则是负数,结果为偶数是正数.
解答 解:由图可知,每5个数为一个循环组依次循环,
所以,“峰n”中峰顶C的位置的数的绝对值5n-1,
当n=202时,5×202-1=1010-1=1009,
∵1009是奇数,
∴“峰202”中C的位置的有理数是-1009;
∵“峰2n+1”峰顶C上的数的绝对值为5(2n+1)-1=10n+5-1=10n+4,
∴“峰2n+1”峰顶B上的数的绝对值为10n+4-1=10n+3,
∵10n+3是奇数,
∴“峰2n+1”中B的位置的数是-(10n+3)=-10n-3.
故答案为:-1009;-10n-3.
点评 本题是对数字变化规律的考查,根据每一个峰有5个数,观察出每5个数为一个循环组依次循环是解题的关键,还要注意正、负数的排列特点.


科目:初中数学 来源: 题型:解答题
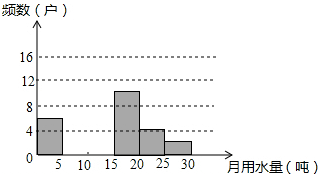 八年级某班同学为了了解2012年某居委会家庭月均用水情况,随机调查了该居委会部分家庭,并将调查数据进行如下调整:
八年级某班同学为了了解2012年某居委会家庭月均用水情况,随机调查了该居委会部分家庭,并将调查数据进行如下调整:| 月均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | a | 0.24 |
| 10<x≤15 | 16 | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | 0.08 |
| 25<x≤30 | 2 | 0.04 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com