
【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别是BE,CD的中点,
(1)求证:△AMN是等边三角形.
(2)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由.

【答案】(1)证明见解析;(2)CD=BE.理由见解析
【解析】试题分析:(1)由等边三角形的性质得到AB=AC,AE=AD, ∠BAC=∠EAD=60°,从而得到BE=CD, 再由中点的定义得到EN=DN, 即有AN=AM, 从而可以得到结论;
(2)可以利用SAS判定△ABE≌△ACD,全等三角形的对应边相等,所以CD=BE.
试题解析:解:(1)∵△ABC和△ADE是等边三角形,∴AB=AC,AE=AD, ∠BAC=∠EAD=60°,
∴AB-AE=AC-AD,即BE=CD, ∴M,N分别是BE,CD的中点,∴EM=![]() BE,DN=
BE,DN=![]() CD, ∴EN=DN, ∴EM+AE=DN+AD,即AN=AM, ∵∠BAC=60°, ∴△AMN是等边三角形;
CD, ∴EN=DN, ∴EM+AE=DN+AD,即AN=AM, ∵∠BAC=60°, ∴△AMN是等边三角形;
(2)CD=BE.理由如下:
∵△ABC和△ADE为等边三角形,∴AB=AC,AE=AD,∠BAC=∠EAD=60°.
∵∠BAE=∠BAC∠EAC=60°∠EAC,∠DAC=∠DAE∠EAC=60°∠EAC,∠BAE=∠DAC,∴△ABE≌△ACD,∴CD=BE.


科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,试判断AC与BC的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用适量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:

(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:u2=﹣x2+mx+n为“友好抛物线”.
(1)求抛物线C2的解析式.
(2)点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a<0)的对称轴为x=1,交x轴的一个交点为(x1,0),且﹣1<x1<0,有下列5个结论:①abc>0;②9a﹣3b+c<0;③2c<3b;④(a+c)2<b2;⑤a+b>m(am+b)(m≠1的实数)其中正确的结论有( )
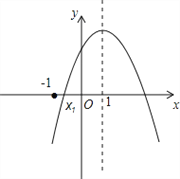
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
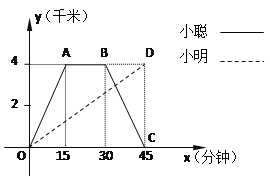
【题目】小聪和小明沿同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系,请根据图象回答下列问题:
(分钟)之间的函数关系,请根据图象回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟,小聪返回学校的速度为 千米/分钟.
(2)请你求出小明离开学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系;
(分钟)之间的函数关系;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实践与操作:
根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).

(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF.
猜想并证明:
判断四边形AECF的形状并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com