
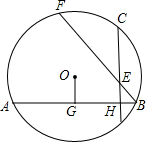
 如图⊙O的弦AB⊥CD于H,D、E关于AB对称,BE延长线交⊙O于F,连接FC,作OG⊥AB于G,则下列结论:①FC=CE,②
如图⊙O的弦AB⊥CD于H,D、E关于AB对称,BE延长线交⊙O于F,连接FC,作OG⊥AB于G,则下列结论:①FC=CE,② |
| AF |
 |
| AD |
| A、①②③ | B、①②④ |
| C、②③④ | D、①②③④ |
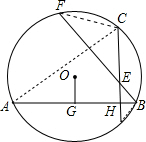 解:连接FC,BD,AC,
解:连接FC,BD,AC, |
| AF |
 |
| AD |


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:单选题
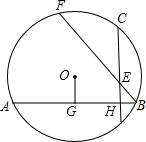 如图⊙O的弦AB⊥CD于H,D、E关于AB对称,BE延长线交⊙O于F,连接FC,作OG⊥AB于G,则下列结论:①FC=CE,②
如图⊙O的弦AB⊥CD于H,D、E关于AB对称,BE延长线交⊙O于F,连接FC,作OG⊥AB于G,则下列结论:①FC=CE,②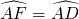 ,③∠B=∠BEH,④△ECF∽△EBD,成立的是
,③∠B=∠BEH,④△ECF∽△EBD,成立的是查看答案和解析>>
科目:初中数学 来源:2011-2012学年重庆市七十九中九年级(上)期中数学试卷(解析版) 题型:选择题
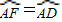 ,③∠B=∠BEH,④△ECF∽△EBD,成立的是( )
,③∠B=∠BEH,④△ECF∽△EBD,成立的是( )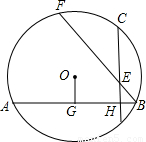
查看答案和解析>>
科目:初中数学 来源:2008-2009学年湖北省武汉市江岸区九年级(上)月考数学试卷(12月份 全册内容)(解析版) 题型:选择题
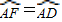 ,③∠B=∠BEH,④△ECF∽△EBD,成立的是( )
,③∠B=∠BEH,④△ECF∽△EBD,成立的是( )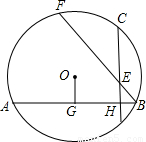
查看答案和解析>>
科目:初中数学 来源: 题型:
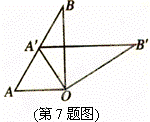
如图⊙O的弦AB⊥CD于H,D、E关于AB对称,BE延长线交⊙O于F,连接FC,作OG⊥AB于G,
则下列结论: ①FC=CE, ②![]() 弧AF=弧AD ,③ OG=
弧AF=弧AD ,③ OG=![]() CF,④GH=BH成立的是( )
CF,④GH=BH成立的是( )
A、①②③ B、①②④ C、②③④ D、①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com