
【题目】如图①,先把一矩形![]() 纸片上下对折,设折痕为
纸片上下对折,设折痕为![]() ;如图②,再把
;如图②,再把
点![]() 叠在折痕线
叠在折痕线![]() 上,得到
上,得到![]()
![]() .过
.过![]() 点作
点作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
(1)求证: ![]() ∽
∽![]() ;
;
(2)在图②中,如果沿直线![]() 再次折叠纸片,点
再次折叠纸片,点![]() 能否叠在直线
能否叠在直线![]() 上?请说明理由;
上?请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的长度.
的长度.

【答案】(1)(2)见解析;(3)![]()
【解析】试题分析:(1)由题意可以得到∠BPE=∠AQB=90°,通过角的转化可以得到∠BEP=∠ABQ,从而可以得到△PBE∽△QAB;
(2)根据折叠的知识可以得到QB=PB,由第(1)问中的相似可以得到对应边成比例,通过转化可以得到△PBE∽△BAE,从而可以解答本题;
(3)由题意和第(2)问可以得到∠AEB=∠BEP=60°,∠ABE=90°,又因为AB=![]() ,sin∠AEB=
,sin∠AEB=![]() ,从而可以得到AE的长度.
,从而可以得到AE的长度.
试题解析:(1)证明:∵PQ⊥MN,BN∥EC∥AD,∴∠BPE=∠AQB=∠PBN=∠NBQ=90°,∴∠PBE+∠BEP=90°,又∵∠PBE+∠ABQ=180°﹣∠ABE=180°﹣90°=90°,∴∠BEP=∠ABQ,在△PBE和△QAB中,∵∠BPE=∠AQB,∠BEP=∠ABQ,∴△PBE∽△QAB;
(2)点A能叠在直线EC上,理由:∵△PBE∽△QAB,∴ ![]() ,∵由折叠可知,QB=PB,∴
,∵由折叠可知,QB=PB,∴![]() ,即
,即![]() ,又∵∠ABE=∠BPE=90°,∴△PBE∽△BAE,∴∠AEB=∠PEB,∴沿直线EB再次折叠纸片,点A能叠在直线EC上;
,又∵∠ABE=∠BPE=90°,∴△PBE∽△BAE,∴∠AEB=∠PEB,∴沿直线EB再次折叠纸片,点A能叠在直线EC上;
(3)解:由(2)可知,∠AEB=∠PEB,而由折叠过程知:2∠AEB+∠PEB=180°,∴∠AEB=∠PEB=60°,在Rt△ABE中,sin∠AEB=![]() ,∴AE=
,∴AE= .
.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查 B. 该校只有360个家长持反对态度
C. 样本是360个家长 D. 该校约有90%的家长持反对态度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随机抽取某城市天的空气质量状况统计如下:
污染指数( |
|
|
|
|
|
|
天数( |
|
|
|
|
|
|
(其中![]() 时,空气质量为优;
时,空气质量为优;![]() 时,空气质量为良;
时,空气质量为良;![]() 时,空气质量为轻微污染)
时,空气质量为轻微污染)
(1)这![]() 天中,空气质量为轻微污染的天数所占的百分数是多少?
天中,空气质量为轻微污染的天数所占的百分数是多少?
(2)估计该城市一年(以![]() 天记)中有多少天空气质量到良以上?
天记)中有多少天空气质量到良以上?
(3)保护环境人人有责,请说出一种保护环境的好方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=3,b=4,c=5; ②a=6,∠A=45°;③a=2,b=2,c=2![]() ; ④∠A=38°,∠B=52°.
; ④∠A=38°,∠B=52°.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列给出的条件中,能判定四边形ABCD为平行四边形的是()
A.AB=BC,CD=DAB.AB//CD,AD=BC
C.AB//CD,∠A=∠CD.∠A=∠B,∠C=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2﹣
x2﹣![]() x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
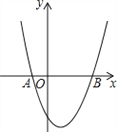
【题目】如图,已知抛物线![]() 经过A(﹣1,0)、B(3,0)两点.
经过A(﹣1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若![]() ,求出此时点P的坐标.
,求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中AC平分∠BAD,∠ADC=∠ACB=90![]() ,E为AB的中点,AC与DE交于点F.
,E为AB的中点,AC与DE交于点F.

(1)求证: ![]() =AB·AD;
=AB·AD;
(2)求证:CE//AD;
(3)若AD=6, AB=8.求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com