
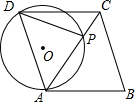
 如图,点P在菱形ABCD的对角线AC上,PA=PD,⊙O为△APD的外接圆.
如图,点P在菱形ABCD的对角线AC上,PA=PD,⊙O为△APD的外接圆.分析 (1)由等腰三角形的性质得出∠PDA=∠PAD.由菱形的性质得出DA=DC.得出∠DAC=∠DCA.因此∠PDA=∠DCA,即可得出结论;
(2)由相似三角形的对应边成比例求出AP=$\frac{9}{2}$,连接PO并延长交AD于点Q,得出PQ垂直平分AD.AQ=3,由勾股定理求出PQ=$\sqrt{A{P}^{2}-A{Q}^{2}}$=$\frac{3\sqrt{5}}{2}$,
连接AO,设半径为r,在Rt△AOQ中,OQ=PQ-r=$\frac{3\sqrt{5}}{2}$-r,由勾股定理得出方程,解方程即可.
解答 (1)证明:∵PA=PD,
∴∠PDA=∠PAD.
∵四边形ABCD是菱形,
∴DA=DC.
∴∠DAC=∠DCA.
∴∠PDA=∠DCA.
∵∠PAD=∠DAC,
∴△APD∽△ADC.
(2)解:∵△APD∽△ADC,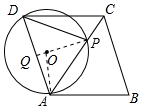
∴$\frac{PA}{AD}=\frac{AD}{AC}$.即$\frac{PA}{6}=\frac{6}{8}$,
解得AP=$\frac{9}{2}$,
连接PO并延长交AD于点Q,
∵PA=PD,
根据圆的轴对称性,得:PQ垂直平分AD.
∴AQ=3,
∴PQ=$\sqrt{A{P}^{2}-A{Q}^{2}}$=$\frac{3\sqrt{5}}{2}$,
连接AO,设半径为r,
在Rt△AOQ中,OQ=PQ-r=$\frac{3\sqrt{5}}{2}$-r,
由勾股定理得:32+($\frac{3\sqrt{5}}{2}$-r)2=r2,
解得:r=$\frac{27\sqrt{5}}{20}$,
即⊙O的半径为$\frac{27\sqrt{5}}{20}$.
点评 本题考查了菱形的性质、相似三角形的判定与性质、三角形的外接圆、勾股定理、等腰三角形的性质等知识;熟练掌握菱形的性质和等腰三角形的性质,证明三角形相似是解决问题的关键.


科目:初中数学 来源: 题型:解答题
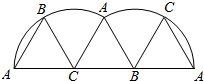 等边三角形ABC的边长是6厘米,在一条直线上将它翻滚几次,使点A再次落在这条直线上.
等边三角形ABC的边长是6厘米,在一条直线上将它翻滚几次,使点A再次落在这条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价(元/台) | 月销售量(台) |
| 400 | 200 |
| 390 | 250 |
| x | -5x+2200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
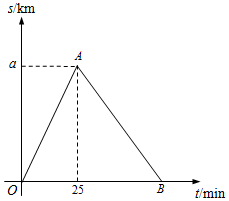 某市举行“迷你马拉松”长跑比赛,运动员从起点甲地出发,跑到乙地后,沿原路线再跑回点甲地.设该运动员离开起点甲地的路程s(km)与跑步时间t(min)之间的函数关系如图所示.已知该运动员从甲地跑到乙地时的平均速度是0.2km/min,根据图象提供的信息,解答下列问题:
某市举行“迷你马拉松”长跑比赛,运动员从起点甲地出发,跑到乙地后,沿原路线再跑回点甲地.设该运动员离开起点甲地的路程s(km)与跑步时间t(min)之间的函数关系如图所示.已知该运动员从甲地跑到乙地时的平均速度是0.2km/min,根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com