
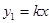 的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数
的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数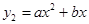 的图象如图②所示.
的图象如图②所示.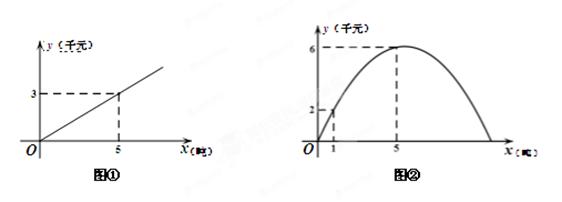
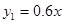 ;
; ;(2)甲种蔬菜进货量为6吨,乙种蔬菜进货量为4吨时,获得的销售利润之和最大,最大利润 是9200元.
;(2)甲种蔬菜进货量为6吨,乙种蔬菜进货量为4吨时,获得的销售利润之和最大,最大利润 是9200元.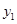 与x之间的关系成一次函数关系,令
与x之间的关系成一次函数关系,令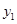 =kx+b,由图知图像经过(0,0),(5,3)两点,带入
=kx+b,由图知图像经过(0,0),(5,3)两点,带入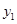 =kx+b求得
=kx+b求得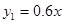 . 由图②知,函数
. 由图②知,函数 与x之间的关系成二次函数关系,可令
与x之间的关系成二次函数关系,可令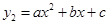 ,由图知此二次函数经过(0,0),(1,2),(5,6)三点,列方程组
,由图知此二次函数经过(0,0),(1,2),(5,6)三点,列方程组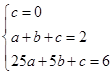 解得
解得
 .
. 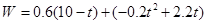 ,
, .
. 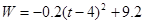 .
. 

科目:初中数学 来源:不详 题型:解答题
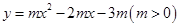 与
与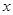 轴交于
轴交于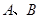 两点,与
两点,与 轴交于
轴交于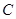 点.
点.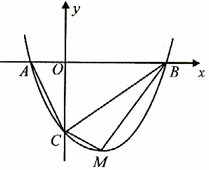
 的坐标(用含
的坐标(用含 的代数式表示),
的代数式表示), 两点的坐标;
两点的坐标;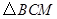 与
与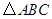 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;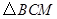 为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 年的维修、保养费用累计为
年的维修、保养费用累计为 (万元),且
(万元),且 ,若第1年的维修、保养费用为2万元,第2年为4万元。
,若第1年的维修、保养费用为2万元,第2年为4万元。 与
与 之间的关系式;
之间的关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
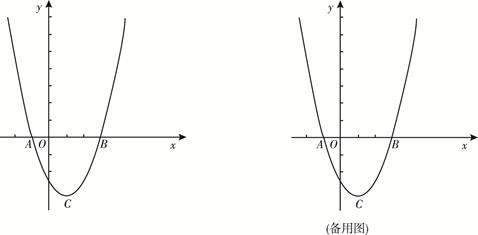
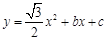 的图象与
的图象与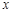 轴交于
轴交于 (-1,0)、
(-1,0)、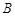 (3,0)两点, 顶点为
(3,0)两点, 顶点为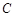 .
.
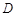 为点
为点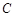 关于x轴的对称点,过点
关于x轴的对称点,过点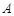 作直线
作直线 :
: 交BD于点E,过点
交BD于点E,过点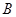 作直线
作直线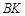 ∥
∥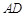 交直线
交直线 于
于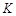 点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;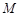 、
、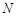 分别为直线
分别为直线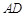 和直线
和直线 上的两个动点,连结
上的两个动点,连结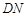 、
、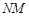 、
、 ,求
,求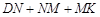 和的最小值.
和的最小值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
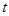 (月)之间的关系(即前
(月)之间的关系(即前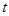 个月的利润总和S与
个月的利润总和S与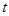 的关系).根据图象提供的信息,解答下列问题.
的关系).根据图象提供的信息,解答下列问题.
 (月)之间的函数关系式;
(月)之间的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
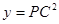 ,则y关于x的函数的图像大致为( )
,则y关于x的函数的图像大致为( )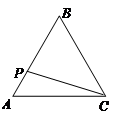
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com