
����Ŀ��ij���ۺ���ʵ����С�鿪չ�˲�����У��˸߶ȵ�ʵ����������ƶ��˲��������������ÿ���ʱ�������ʵ�ز���.��������˵ײ����ڵ�ƽ���ϣ�ѡȡ������ͬ��㣬�ֱ�����˸���˶��˵������Լ����������֮��ľ���.Ϊ�˼�С������С���ڲ������ǵĶ����Լ��������֮��ľ���ʱ�����ֱ���������β�ȡ���ǵ�ƽ��ֵ��Ϊ��������������������±�(������)
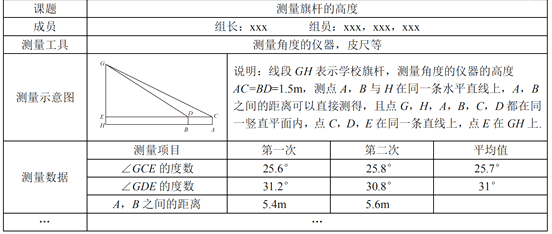

����һ�����β���A��B֮��ľ����ƽ��ֵ�� m.
��������������ϲ������������������ۺ���ʵ����С�����ѧУѧУ���GH�ĸ߶�.
(�ο����ݣ�sin25.7���0.43��cos25.7���0.90��tan25.7���0.48��sin31���0.52��cos31���0.86��tan31���0.60)
�������������ۺ���ʵ����С���ڶ��Ʒ���ʱ�����۹������������������µ�Ӱ�Ӳ�����˵ĸ߶����ķ�������δ������.����Ϊ��ԭ�������ʲô��(д��һ������).
���𰸡�����һ��5.5������������GH�ĸ߶�Ϊ14.7m����������������.
��������
����һ������ƽ������ʽ���м��㼴�ɵã�
�������������ɵã��ı���ACDB���ı���ACEH���Ǿ��Σ�����EH=AC=1.5��CD=AB=5.5����EG=x m����Rt��DEG�У����á�GDE�����пɵ�![]() ����Rt��CEG�У����á�GCE�����пɵ�CE=
����Rt��CEG�У����á�GCE�����пɵ�CE=![]() ���ٸ���CD=CE-DE�������x��ֵ���ٸ���GH=CE+EH������ô𰸣�
���ٸ���CD=CE-DE�������x��ֵ���ٸ���GH=CE+EH������ô𰸣�
��������д��������ֻҪ��������.
����һ��![]() =5.5(m)��
=5.5(m)��
�ʴ�Ϊ��5.5��
�������������ɵã��ı���ACDB���ı���ACEH���Ǿ��Σ�
��EH=AC=1.5��CD=AB=5.5��
��EG=x m��
��Rt��DEG����DEC=90������GDE=31����
��tan31��=![]() ����
����![]() ��
��
��Rt��CEG����CEG=90������GCE=25.7����
��tan25.7��=![]() ����CE=
����CE=![]() ��
��
��CD=CE-DE��
��![]() ��
��
��![]() ��
��
��GH=CE+EH=13.2+1.5=14.7��
�����GH�ĸ߶�Ϊ14.7m��
���������𰸲�Ψһ��û��̫���⣬��˵ײ����ɵ���������Ӱ�ӵij����������ѵ�.


 ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y��ax2��bx��c(a��0)��ͼ����A��B��C�����������ĸ��ƶϣ��������߿������£��ڵ�x=��2ʱ��yȡ���ֵ���۵�m<4ʱ������x��һԪ���η���ax2��bx��c=m������������ȵ�ʵ��������ֱ��y=kx+c(k��0)������A��C����kx+c> ax2��bx��cʱ��x��ȡֵ��Χ�ǣ�4<x<0�������ƶ���ȷ���� �� ��
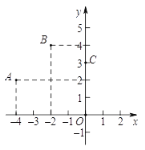
A. �٢�B. �٢�C. �٢ۢ�D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
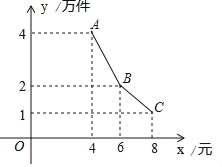
����Ŀ��Ϊ��֧�ִ�ѧ����ҵ��ij��������̨��һ���Ż����ߣ��ṩ10��Ԫ����Ϣ��ҵ���С��������ʴ��ע����һ���Ա����꣬����5��Ա��������һ�ֻ𱬵ĵ��Ӳ�Ʒ����Լ���ø����꾭Ӫ���������³��������Ϣ�����֪�ò�Ʒ�ijɱ�Ϊÿ��4Ԫ��Ա��ÿ��ÿ�µĹ���Ϊ4ǧԪ�������껹��ÿ��֧����������1��Ԫ���ò�Ʒÿ��������y������������۵���x��Ԫ�����֮��ĺ�����ϵ��ͼ��ʾ��
��1���������ÿ������w����Ԫ�������۵���x��Ԫ��֮��ĺ�������ʽ��
��2��С�������꿪ҵ������ڵڼ����¿ɻ���10��Ԫ����Ϣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ƕ��κ������Һ���ͼ������ߵ㣮
�Ƕ��κ������Һ���ͼ������ߵ㣮
��1����![]() ��ֵ��
��ֵ��
��2����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��![]() ����������٣�
����������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A����1��0������y��Ľ���B�ڣ�0����2���ͣ�0����1��֮�䣨�����������㣩���Գ���Ϊֱ��x=1�����н��ۣ���abc��0 ��4a+2b+c��0 ��4ac��b2��8a ��![]() ��a��
��a��![]() ��b��c�����к�������ȷ���۵�ѡ���ǣ�������
��b��c�����к�������ȷ���۵�ѡ���ǣ�������
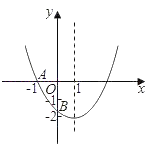
A. �٢� B. �٢ۢ� C. �ڢܢ� D. �٢ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
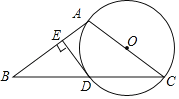
����Ŀ����ͼ���ڵ�����ABC�У�AB��AC����ACΪֱ������O��BC�ڵ�D������D��DE��AB������ΪE��
��1����֤��DE�ǡ�O�����ߣ�
��2����DE![]() ����C��30������
����C��30������![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽����
��ͼ��ʾ����ƽ��ֱ������ϵ�У�ֱ��![]() �뷴��������
�뷴��������![]() ��ͼ����
��ͼ����![]() ��
��![]() ���㣬����
���㣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��

��1����![]() ��
��![]() ��ֵ�������������ĺ�������ʽ��
��ֵ�������������ĺ�������ʽ��
��2������![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ���������ʱ��
���������ʱ��![]() �����ꣻ
�����ꣻ
��3��Сӱ��̽���з��֣���![]() ���������ϴ��ڵ�
���������ϴ��ڵ�![]() ��ʹ��
��ʹ��![]() ����
����![]() Ϊ���ǵĵ���������.����ֱ��д����
Ϊ���ǵĵ���������.����ֱ��д����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����д�����չ������β�ҵ��ȫ������Ͷ�������������������ͼ��������ͼ��Ļ����ͼ���ʳ������ȫʡ���������ﲻ����ȥ������ij�����ץס������Ͷ��20��Ԫ����ũ���֣�����+ס�ޣ���һ��ʱ����ջ�Ͷ�ʵ�80%�����в���������ס�������2������1��Ԫ��
��1����ȥ���ũ���ֲ�����ס�������Ϊ������Ԫ��
��2������ô������Ͷ����10��Ԫ�����������ز���ʵ�����ۺ�����������Ŀ��ʵ��ӯ���������ڽ��ܼ��߲ɷ�ʱ˵��Ԥ�ƽ��������ס�������ȥ�껹����10%����������������������ȥ����Ͷ����ܻ�ò�����10��Ԫ�Ĵ��������ʽ������ز������������������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ������
������![]() �ӵ�
�ӵ�![]() ��������
��������![]() ���������˶����ٶ�Ϊ
���������˶����ٶ�Ϊ![]() ��ͬʱ������
��ͬʱ������![]() �ӵ�
�ӵ�![]() ��������
��������![]() ���������˶����ٶ�Ϊ
���������˶����ٶ�Ϊ![]() ����һ����ֹͣ�˶�����һ����Ҳֹͣ�˶������
����һ����ֹͣ�˶�����һ����Ҳֹͣ�˶������![]() ��
��![]() �˶���ʱ����
�˶���ʱ����![]()
![]()
![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��
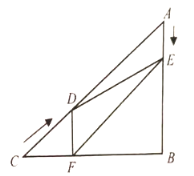
��1��![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��
��2�����ı���![]() �����Ϊ
�����Ϊ![]() �������
�������![]() ��
��![]() ֮��Ĺ�ϵʽ��
֮��Ĺ�ϵʽ��
��3���Ƿ����ijһʱ��![]() ��ʹ��
��ʹ��![]() �����ڣ����
�����ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
��4����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com