
【题目】如图,已知⊙O为△ABC(∠A<∠ABC)的外接圆,且AB为![]() 的直径,AB=8,点D为AB延长线上一点,点 E为半径OB上一点,连接CD、CE、OC,且∠BCD=∠A.
的直径,AB=8,点D为AB延长线上一点,点 E为半径OB上一点,连接CD、CE、OC,且∠BCD=∠A.

(1)求证:CD为![]() 的切线;
的切线;
(2)若CB=CE,求证:CE2=CO2-OA·OE;
(3)在(2)的条件下,求OE+BC的最大值.
【答案】(1)见解析;(2)见解析;(3)OE+BC有最大值为5.
【解析】
(1)运用圆的性质和角的和差,确定∠OCD=∠BCD+∠BCO=90°,即可证明;(2)先证明△OBC∽△CBE,运用其性质结合等量代换即可解答.(3)设BC=x,AB=8,∴OA=OC=4,结合(2)的结论,求二次函数的最小值即可;
解:(1)∵AB为⊙O直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,
又∵OA=OC,∴∠A=∠ACO,
∵∠BCD=∠A,∴∠BCD+∠BCO=90°,∴CD为⊙O切线;
(2)∵CE=CB,∴∠CEB=∠CBE,
又OC=OB,∴∠OCB=∠OBC,
∴△OBC∽△CBE,
∴![]() ,即BC2=BE·OB,
,即BC2=BE·OB,
又BC=EC,OB=OC=OA,
∴CE2=(OB-OE)·OB= CO2-OA·OE;
(3)设BC=x,∵AB=8,∴OA=OC=4,
由(2)知x2=16-4OE,∴OE=![]() ,
,
∴OE+BC=![]() =
=![]() ,
,
∵∠A<∠ABC,
∴0<x<![]() ,
,
∴当x=2时,OE+BC有最大值为5.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】已知,抛物线C1:y=- ![]() x2+mx+m+
x2+mx+m+ ![]()
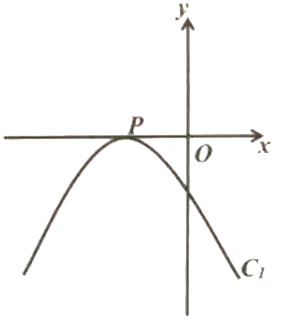
(1)①当m=1时,抛物线与x轴的交点坐标为_______;②当m=2时,抛物线与x轴的交点坐标为________;
(2)①无论m取何值,抛物线经过定点P________;②随着m的取值的变化,顶点M(x,y)随之变化,y是x的函数,记为函数C2 , 则函数C2的关系式为:________;
(3)如图,若抛物线C1与x轴仅有一个公共点时,①直接写出此时抛物线C1的函数关系式;②请在图中画出顶点M满足的函数C2的大致图象,在x轴上任取一点C,过点C作平行于y轴的直线l分别交C1、C2于点A、B,若△PAB为等腰直角三角形,求点C的坐标;
(4)二次函数的图象C2与y轴交于点N,连接PN,若二次函数的图象C1与线段PN有两个交点,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的
一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运
动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为
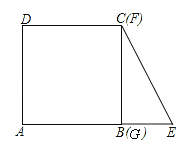
A.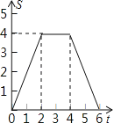 B.
B.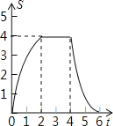
C.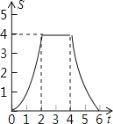 D.
D.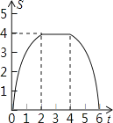
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,(k为常数,k≠1).
,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时.数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速在l外取一点P,作PC⊥1,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°,测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速?(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
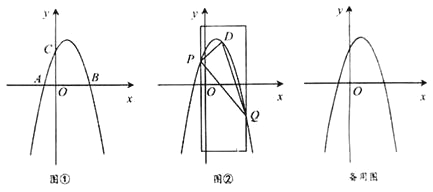
【题目】如图①,在平面直角坐标系xOy 中,抛物线y=ax2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y轴交于点C
.
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、 Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP、DQ.
①若点P的横坐标为![]() ,求△DPQ面积的最大值,并求此时点D 的坐标;
,求△DPQ面积的最大值,并求此时点D 的坐标;
②直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
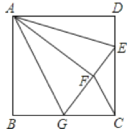
【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则BG的长为( )
A. 1B. 2C. 1.5D. 2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对学生进行革命传统教育,红旗中学开展了“清明节祭扫”活动.全校学生从学校同时出发,步行![]() 米到达烈士纪念馆.学校要求九
米到达烈士纪念馆.学校要求九![]() 班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的
班提前到达目的地,做好活动的准备工作.行走过程中,九(1)班步行的平均速度是其他班的![]() 倍,结果比其他班提前
倍,结果比其他班提前![]() 分钟到达.分别求九(1)班、其他班步行的平均速度.
分钟到达.分别求九(1)班、其他班步行的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,矩形ABOC的边BO在x轴的负半轴上,边OC在y轴的正半轴上,且AB=1,OB=![]() ,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.
,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.
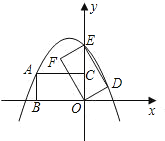
(1)判断点E是否在y轴上,并说明理由;
(2)求抛物线的函数表达式;
(3)在x轴的上方是否存在点P,点Q,使以点O,B,P,Q为顶点的平行四边形的面积是矩形ABOC面积的2倍,且点P在抛物线上?若存在,请求出点P,点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com