
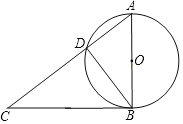
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,连接BD.
(1)求证:∠A=∠CBD.
(2)若AB=10,AD=6,M为线段BC上一点,请写出一个BM的值,使得直线DM与⊙O相切,并说明理由.
【答案】(1)证明见解析;(2)BM=![]() ,理由见解析.
,理由见解析.
【解析】
(1)利用圆周角定理得到∠ADB=90°,然后就利用等角的余角相等得到结论;
(2)如图,连接OD,DM,先计算出BD=8,OA=5,再证明Rt△CBD∽Rt△BAD,利用相似比得到BC=![]() ,取BC的中点M,连接DM、OD,如图,证明∠2=∠4得到∠ODM=90°,根据切线的判定定理可确定DM为⊙O的切线,然后计算BM的长即可.
,取BC的中点M,连接DM、OD,如图,证明∠2=∠4得到∠ODM=90°,根据切线的判定定理可确定DM为⊙O的切线,然后计算BM的长即可.
(1)∵AB为⊙O直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°.
∵∠ABC=90°,
∴∠CBD+∠ABD=90°,
∴∠A=∠CBD;
(2)BM=![]() .
.
理由如下:
如图,连接OD,DM,
∵∠ADB=90°,AB=10,AD=6,
∴BD=![]() =8,OA=5,
=8,OA=5,
∵∠A=∠CBD,
∵Rt△CBD∽Rt△BAD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得BC=
,解得BC=![]()
取BC的中点M,连接DM、OD,如图,
∵DM为Rt△BCD斜边BC的中线,
∴DM=BM,
∵∠2=∠4,
∵OB=OD,
∴∠1=∠3,
∴∠1+∠2=∠3+∠4=90°,即∠ODM=90°,
∴OD⊥DM,
∴DM为⊙O的切线,
此时BM=![]() BC=
BC=![]() .
.



科目:初中数学 来源: 题型:
【题目】为了提高农民抵御大病风险的能力,全国农村推行了新型农村合作医疗政策,农民只需每人每年交10元钱,就可以加入合作医疗.若农民患病住院治疗,出院后到新型农村合作医疗办公室按一定比例报销医疗费.小军与同学随机调查了他们镇的一些村民,根据收集到的数据绘制成了如图所示的统计图.

根据以上信息,解答下列问题:
(1)本次共调查了多少村民被调查的村民中,有多少人参加合作医疗得到了报销款?
(2)若该镇有村民10000人,请你计算有多少人参加了合作医疗?要使两年后参加合作医疗的人数增加到9680人,假设这两年的年增长率相同,求这个年增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
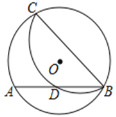
【题目】如图, 在⊙O 中,点 C 在优弧 AB 上, 将弧 BC 沿 BC 折叠后刚好经过 AB的中点 D. 若⊙O的半径为![]() ,AB=4,则 BC 的长是( )
,AB=4,则 BC 的长是( )
A.2![]() B.3
B.3![]() C.4D.2
C.4D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
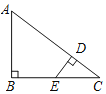
【题目】如图,Rt△ABC中,∠B=90°,点D在边AC上,且DE⊥AC交BC于点E.
(1)求证:△CDE∽△CBA;
(2)若AB=3,AC=5,E是BC中点,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
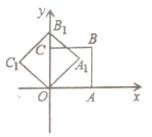
【题目】如图,在平面直角坐标系中,将正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到正方形
后得到正方形![]() ,依此方式,绕点
,依此方式,绕点![]() 连续旋转2019次得到正方形
连续旋转2019次得到正方形![]() ,如果点
,如果点![]() 的坐标为(1,0),那么点
的坐标为(1,0),那么点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.

(1)请判断:FG与CE的数量关系是__________,位置关系是__________;
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com