
����Ŀ������֪������һ��ͼ�Σ�ͨ����ͬ�ķ�������ͼ�ε����ʱ�����Եõ�һ����ѧ��ʽ��������ͼ1���Եõ�![]() ����ش��������⣺
����ش��������⣺

��1��д��ͼ2������ʾ����ѧ��ʽ�� ��
��2����ͼ3�����Ŀ���ȫ��ͬ�ij�����ƴ�������Σ��ò�ͬ�ķ���������ͼ����Ӱ���ֵ���������ܷ���ʲô?(�ú���![]() ��
��![]() ��ʽ�ӱ�ʾ) ��
��ʽ�ӱ�ʾ) ��
��3��ͨ�������ĵ�����ϵ�����ǿ�֪: �����������ĺ�һ��ʱ�����ǵIJ�ľ���ֵԽС�����Խ ������ ����������С�����������������Ļ�һ��ʱ�����ǵIJ�ľ���ֵԽС�����Խ ������ ��������С������
���𰸡���1��![]() ����2��
����2��![]() ��
��
��3���� С
��������
��1��ͼ2����������������ɳ�Ϊ2a+b����Ϊa+2b�ľ�����������Ҳ�����������߳�Ϊa��߳�Ϊb���������Σ���4����Ϊa����Ϊb�ľ������֮���������ʾ���ɣ�
��2����Ӱ���ֵ���������ɱ߳�Ϊx+y�Ĵ������ε������ȥ�߳�Ϊx-y��С��������������Ҳ������4����Ϊx����Ϊy�ľ������֮���������ʾ�����ɣ�
��3����������һ������͵�ƽ��һ�������ݵ�ʽ![]() ���õ�������һ������ľ���ֵԽС����Ϊ����ԽС���õ���Խ����Խ����������һ��ʱ������һ������ľ���ֵԽС���õ�����ԽС���ɵó�������ԽС��
���õ�������һ������ľ���ֵԽС����Ϊ����ԽС���õ���Խ����Խ����������һ��ʱ������һ������ľ���ֵԽС���õ�����ԽС���ɵó�������ԽС��
��1����ͼ��֪��![]()
��2��![]()
��3�������������ĺ�һ��ʱ�����ǵIJ�ľ���ֵԽС���Խ�����������Ļ�һ��ʱ�����ǵIJ�ľ���ֵԽС���ԽС.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AD��BC���ϵ����ߣ�AE��BC���ϵĸߣ�
��1������ACB��100�������CAE�Ķ�����
��2����S��ABC��12��CD��4�����AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ���̻�У,�ƻ�����һ��������������,���г�����,�����ĵ��۱���������20Ԫ,����3��������2������������340Ԫ.
(1)�������������ĵ��۸��Ƕ���?
(2)����ѧУʵ�����,�蹺���������繲150��,�ܷ��ò�����10840Ԫ,�ҹ����������Ŀ���������������1.5��,���������У���ι��������������������ļ��ַ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ��ֻ�Ӧ��ͼ���У�������Գ�ͼ���������ĶԳ�ͼ�ε��ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
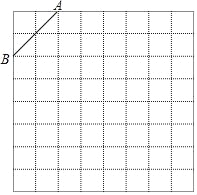
����Ŀ����ͼ�ǹ��Ϊ8��8�������������������������а�����Ҫ�������
(1)�������н���ƽ��ֱ������ϵ��ʹA������Ϊ(��2��4)��B������Ϊ(��4��2)��
(2)�ڵڶ������ڵĸ���ϻ�һ��C��ʹ��C���߶�AB���һ����ABΪ�ĵ��������Σ�������������������C���������� ����
(3)���ABC��BC���ϵĸ߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���A��2��0������B��0��1��������A��ֱ��l��ֱ���߶�AB����P��ֱ��l��һ���㣬����P��PC��x�ᣬ����ΪC���ѡ�ACP��AP����180�㣬ʹ��C���ڵ�D��������A��D��PΪ��������������ABP���ƣ�����������������ĵ�P������Ϊ �� 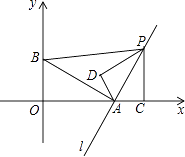
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
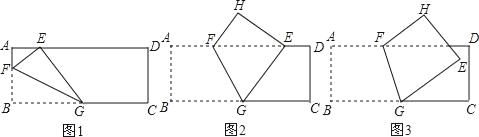
����Ŀ����ͼ��������ֽƬABCD�У�AB��8����ֽƬ�۵���ʹ����B���ڱ�AD�ϵ�E�㴦���ۺ۵�һ��G���ڱ�BC�ϣ�
(1)��ͼ1�����ۺ۵���һ��F��AB������AE��4ʱ����AF�ij�
(2)��ͼ2�����ۺ۵���һ��F��AD������BG��10ʱ��
����֤��EF��EG������AF�ij���
(3)��ͼ3�����ۺ۵���һ��F��AD���ϣ�B��Ķ�Ӧ��E�ڳ������ڲ���E��AD�ľ���Ϊ2cm����BG��10ʱ����AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABC��������ABC����8��8�����У�λ����ͼ��ʾ��A����3��1����B����2��4����

��1�������ڷ����н���ֱ������ϵ����д��C������ꣻ
��2���ѡ�ABC����ƽ��1����λ���ȣ�������ƽ��2����λ���ȣ����㻭��ƽ�ƺ�ġ�A1B1C1������ABC�ڲ�һ��P������Ϊ��a��b�������P�Ķ�Ӧ��P1�������� ��
��3����x���ϴ���һ��D��ʹ��DB1C1���������3�������������ĵ�D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ��a��b�������϶�Ӧ���λ����ͼ��ʾ������|a|+ ![]() �Ľ���ǣ� ��
�Ľ���ǣ� ��![]()
A.��2a+b
B.2a��b
C.��b
D.b
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com