
分析 根据抛物线与x轴有两个不同的交点,根的判别式△>0,再分a>0和a<0两种情况对③④选项讨论即可得解.
解答 解:①∵二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点坐标分别为(x1,0),(x2,0),
∴△=b2-4ac>0,故本选项正确;
②∵点M(x0,y0)在二次函数y=ax2+bx+c(a≠0)的图象上,
∴x=x0是方程ax2+bx+c=y0的解,故本选项正确;
③若a>0,则x1<x0<x2,
若a<0,则x0<x1<x2或x1<x2<x0,故本选项错误;
④若a>0,则x0-x1>0,x0-x2<0,
所以,(x0-x1)(x0-x2)<0,
∴a(x0-x1)(x0-x2)<0,
若a<0,则(x0-x1)与(x0-x2)同号,
∴a(x0-x1)(x0-x2)<0,
综上所述,a(x0-x1)(x0-x2)<0正确,故本选项正确.
故①②④正确,
故答案为①②④
点评 本题考查了二次函数与x轴的交点问题,熟练掌握二次函数图象以及图象上点的坐标特征是解题的关键,③④选项要注意分情况讨论.


科目:初中数学 来源: 题型:解答题
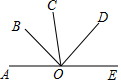 如图所示,A、O、E三点在同一条直线上,OB平分∠AOC,OD平分∠EOC.
如图所示,A、O、E三点在同一条直线上,OB平分∠AOC,OD平分∠EOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
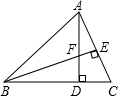 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com