
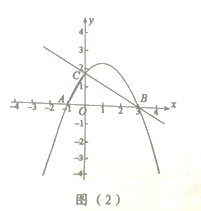
【题目】如图1,在平面直角坐标系中,![]() 为原点,抛物线
为原点,抛物线![]() 经过
经过![]() 三点,且其对称轴为
三点,且其对称轴为![]() 其中点
其中点![]() ,点
,点![]() .
.

(1)求抛物线的解析式;
(2)①如图(1),点![]() 是直线
是直线![]() 上方抛物线上的动点,当四边形
上方抛物线上的动点,当四边形![]() 的面积取最大值时,求点
的面积取最大值时,求点![]() 的坐标;
的坐标;
②如图(2),连接![]() 在抛物线上有一点
在抛物线上有一点![]() 满足
满足![]() ,请直接写出点
,请直接写出点![]() 的横坐标.
的横坐标.
【答案】(1)![]() ;(2)①D
;(2)①D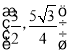 ,②
,②![]() 或
或![]()
【解析】
(1)根据点![]() ,点
,点![]() ,利用待定系数法,可得函数解析式;
,利用待定系数法,可得函数解析式;
(2)①先求出直线BC的解析式,当直线m与抛物线只有一个交点时,点D到BC的距离最远,此时△BCD取最大值,故四边形DCAB有最大值,求出b的值代入原式即可得到答案;
②根据题干条件抛物线上有一点![]() 满足
满足![]() ,通过利用待定系数法利用方程组求出直线BE的解析式,可得答案.
,通过利用待定系数法利用方程组求出直线BE的解析式,可得答案.
解:(1)由题意得:
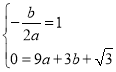
解得![]()
故抛物线的解析式是![]() .
.
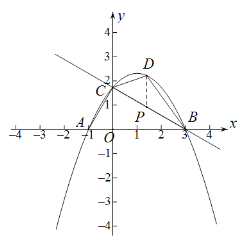
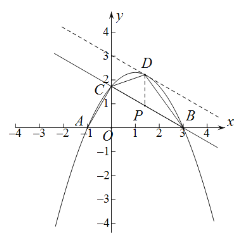
图(1) 图(2)
(2)①设直线BC的解析式为y=kx+![]() .
.
∵直线BC过点B(3,0),
∴0=3k+![]()
则k=![]() ,
,
故直线BC解析式为y=![]() x+
x+![]() .
.
设直线m解析式为![]() ,且直线m∥直线BC
,且直线m∥直线BC
当直线m与抛物线只有一个交点时,点D到BC的距离最远,此时△BCD取最大值,故四边形DCAB有最大值.
令![]() ,
,
![]()
当![]() 时
时
直线m与抛物线有唯一交点
解之得:![]()
代入原式可求得:![]()
∴D![]()
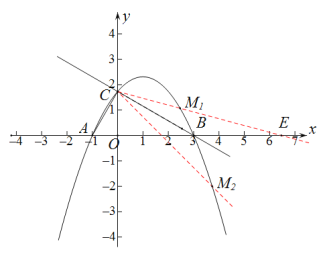
图(3)
过D作DP∥y轴交CB于点P,△DCB面积=△DPC面积+△DPB面积,
∴D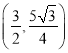
②存在,点M的横坐标为![]() 或
或![]()
解题提示:如图3
符合条件的直线有两条: CM1和CM2(分别在CB的上方和下方)
∵在Rt△ACO中,∠ACO=30°,在Rt△COB中,∠CBO=30°,
∴∠BCM1=∠BCM2=15°
∵△BCE中,∠BCE=∠BEC2=15°
∴BC=BE=![]()
则E(![]() ,0)
,0)
设直线CE解析式为:![]()
∴![]()
解之得:k=![]()
∴直线CE解析式为:![]()
∴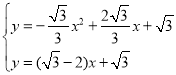
解得:x1=0,x2=2![]() -1
-1
∵ 在Rt△OCF中,∠CBO=30°,∠BCF=15°
∴在Rt△COF中, ∠CFO=45°
∴OC=OF=![]()
∴F(![]() ,0)
,0)
∴直线CF的解析式为![]()
∴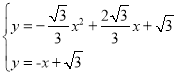
解之得:![]() (舍去),
(舍去),![]()
即点M的横坐标为:![]() 或
或![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=![]() .
.
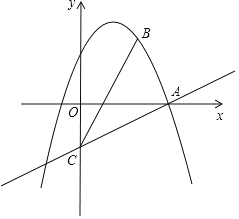
(1)求这条抛物线的表达式及对称轴;
(2)联结AB、BC,求∠ABC的正切值;
(3)若点D在x轴下方的对称轴上,当S△DBC=S△ADC时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查越城区2019年空气质量情况,小强同学从区环保局调取了2019年全年365天的空气质量(AQI)数据,并从中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表,请根据图表中提供的信息解答下列问题:
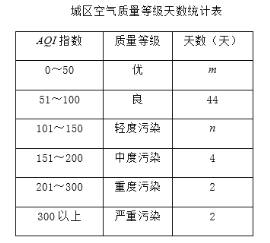
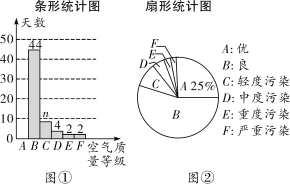
(1)请求出统计表中m、n的值;
(2)补全条形统计图,并通过计算估计越城区2019年全年空气质量等级为“优”和“良”的天数;
(3)据调查,严重污染的2天发生在春节期间,燃放烟花爆竹成为空气污染的一个重要原因.据此,请你提出一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 上依次有
上依次有![]() 三点,
三点,![]() 的延长线交
的延长线交![]() 于
于![]() 过点
过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() 连
连![]() 交
交![]() 于点
于点![]() .
.
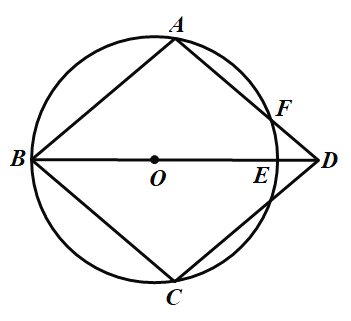
(1)求证:四边形![]() 是菱形;
是菱形;
(2)连接![]()
![]() 当
当![]()
![]() 时,点
时,点![]() 为弧
为弧![]() 的中点;
的中点;
![]() 若
若![]() 且
且![]() ,则
,则![]() 的半径是 .
的半径是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到社会的广泛关注,某校政教处对部分学生就校园安全知识的了解程度,进行了随机抽样调查,并绘制了如下两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有______名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
对于两个正数a、b,则![]() (当且仅当a=b时取等号).
(当且仅当a=b时取等号).
当![]() 为定值时,
为定值时,![]() 有最小值;当
有最小值;当![]() 为定值时,
为定值时,![]() 有最大值.
有最大值.
例如:已知![]() ,若
,若![]() ,求
,求![]() 的最小值.
的最小值.
解:由![]() ≥
≥![]() ,得
,得![]() ≥
≥![]() ,当且仅当
,当且仅当![]() 即
即![]() 时,
时,![]() 有最小值,最小值为
有最小值,最小值为![]() .
.
根据上面的阅读材料回答下列问题:
(1)已知![]() ,若
,若![]() ,则当
,则当![]() 时,
时,![]() 有最小值,最小值为 ;
有最小值,最小值为 ;
(2)已知![]() ,若
,若![]() ,则
,则![]() 取何值时,
取何值时,![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
(3)用长为![]() 篱笆围一个长方形花园,问这个长方形花园的长、宽各为多少时,所围的长方形花园面积最大,最大面积是多少?
篱笆围一个长方形花园,问这个长方形花园的长、宽各为多少时,所围的长方形花园面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是七年级二班参加社团活动人数的扇形统计图(每位同学只参加其中一个社团).根据统计图提供的信息,下列结论正确的是( )
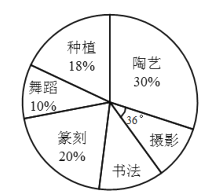
A. 参加摄影社的人数占总人数的![]()
B. 参加篆刻社的扇形的圆心角度数是![]()
C. 参加种植社的同学比参加舞蹈社的多![]() 人
人
D. 若参加书法社的人数是![]() 人,则该班有
人,则该班有![]() 人
人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com