
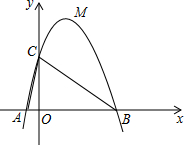
 如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1
如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1分析 (1)由抛物线的对称性可求得A(-1,0),设抛物线的解析式为y=a(x-3)(x+1),将点C的坐标代入可求得a的值,从而可求得抛物线的解析式;(2)过点M作MD⊥AB,交CD与点D,过点M作ME⊥CB,垂足为E.设点M的坐标为(x,-x2+2x+3),先求得直线BC的解析式,然后可得到MD与x的函数关系式,依据二次函数的性质可求得MD的最大值,从而可求得△BCM的最大值,然后依据三角形的面积公式可求得ME的最大值;
(3)连接DP,过点P作PE⊥QD,垂足为E,然后可证明点Q、P、B、D共圆,从而可证明∠PDQ=∠ACO或∠PDQ=∠CAO,设点P的坐标为(x,-x2+2x+3),则PE=x-1,DE=-x2+2x+3.接下来,依据$\frac{EP}{ED}$=$\frac{1}{3}$或$\frac{EP}{ED}$=3列出关于x的方程,从而可求得点P的坐标.
解答 解:(1)∵抛物线的对称轴为x=1,B(3,0),
∴A(-1,0).
设抛物线的解析式为y=a(x-3)(x+1).
将点C的坐标代入得:-3a=3,解得a=-1,
∴抛物线的解析式为y=-x2+2x+3.
(2)设点M的坐标为(x,-x2+2x+3).
设直线BC的解析式为y=kx+3,将点B的坐标代入得:3k+3=0,解得:k=-1,
∴直线BC的解析式为y=-x+3.
如图1所示:过点M作MD⊥AB,交CD与点D,过点M作ME⊥CB,垂足为E.
MD=-x2+2x+3-(-x+3)=-x2+3x.
所以当x=$\frac{3}{2}$时,MD有最大值$\frac{9}{4}$.
在Rt△BCO中,依据勾股定理可知BC=3$\sqrt{2}$.
∴BC•EM=DM•OB,即3$\sqrt{2}$ME=$\frac{9}{4}$×3,解得ME=$\frac{9\sqrt{2}}{8}$.
所以M到BC的最大距离为$\frac{9\sqrt{2}}{8}$.
(3)如图3所示:连接DP,过点P作PE⊥QD,垂足为E.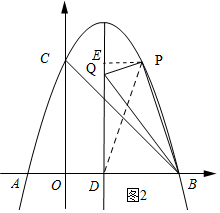
∵∠QPB=∠QDB=90°,
∴∠QPB+∠QDB=180°.
∴点Q、P、B、D共圆.
∴∠PBQ=∠PBQ.
∵以P点为直角顶点的△PBQ与△AOC相似,
∴∠PBQ=∠ACO或∠PBQ=∠CAO.
∴∠PDQ=∠ACO或∠PDQ=∠CAO.
设点P的坐标为(x,-x2+2x+3),则PE=x-1,DE=-x2+2x+3.
∵当∠PDQ=∠ACO时,tan∠ACO=$\frac{AO}{OC}$=$\frac{1}{3}$,
∴$\frac{EP}{ED}$=$\frac{x-1}{-{x}^{2}+2x+3}$=$\frac{1}{3}$,解得:x=2或x=-3(舍去)
所以点P的坐标为(2,3).
当∠PDQ=∠CAO时,tan∠ACO=$\frac{AO}{OC}$=3,
∴$\frac{EP}{ED}$=$\frac{x-1}{-{x}^{2}+2x+3}$=3,解得:x=$\frac{5+\sqrt{145}}{6}$或x=$\frac{5-\sqrt{145}}{6}$(舍去).
∴点P的坐标为($\frac{5+\sqrt{145}}{6}$,$\frac{\sqrt{145}-1}{18}$).
同理:当点P在第象限时,$\frac{EP}{ED}$=3或$\frac{EP}{ED}$=$\frac{1}{3}$.
当$\frac{x-1}{{x}^{2}-2x-3}$=3时,解得:x=$\frac{7+\sqrt{145}}{6}$
∴P的坐标为($\frac{7+\sqrt{145}}{6}$,-$\frac{\sqrt{145}+1}{18}$).
当$\frac{x-1}{{x}^{2}-2x-3}$=$\frac{1}{3}$时,解得x=0(舍去)或x=5.
∴点P的坐标为(5,-12).
综上所述点P的坐标为(2,3)或($\frac{5+5\sqrt{5}}{6}$,$\frac{5\sqrt{5}-1}{18}$或(5,-12)或($\frac{7+\sqrt{145}}{6}$,-$\frac{\sqrt{145}+1}{18}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了二次函数的性质、相似三角形的性质,用含x的式子表示出相关线段的长度是解题的关键.


科目:初中数学 来源: 题型:解答题
| 素质测试 | 测试成绩 | |||
| 李兵 | 张军 | 赵海 | 王洋 | |
| 计算机 | 70 | 80 | 75 | 70 |
| 商品知识 | 60 | 65 | 75 | 65 |
| 语言 | 80 | 75 | 70 | 75 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
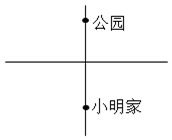 如图,小明周末到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( )
如图,小明周末到公园走到十字路口处,记不清前面哪条路通往公园,那么他能一次选对路的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
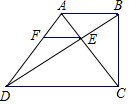 如图,在四边形ABCD中,AB∥CD,∠ABC=90°,CD=2AB,对角线AC与BD相交于点E,EF∥CD交AD于点F.
如图,在四边形ABCD中,AB∥CD,∠ABC=90°,CD=2AB,对角线AC与BD相交于点E,EF∥CD交AD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
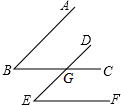 已知:①如图,AB∥DE,BC∥EF,BC与DE相交于点G.请你猜想∠B与∠E之间具有什么数量关系,并说明理由.②请猜测:如果一个角的两条边与另一个角的两条边分别平行,那么这两个角的数量关系是相等或互补.
已知:①如图,AB∥DE,BC∥EF,BC与DE相交于点G.请你猜想∠B与∠E之间具有什么数量关系,并说明理由.②请猜测:如果一个角的两条边与另一个角的两条边分别平行,那么这两个角的数量关系是相等或互补.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -52 与(-5)2相等 | |
| B. | 如果两个数的和为零,那么这两个数一定是一正一负 | |
| C. | -a2表示一个负数 | |
| D. | 两个有理数的差不一定小于被减数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com