
【题目】浙江省委十三届四次全会提出,要以治污水、防洪水、排涝水、保供水、抓节水“五水共治”的重大决策,某中学为了提高学生参与“五水共治”的积极性举行了“五水共治”知识竞赛,所有参赛学生分别设有一、二、三等奖和纪念奖,获奖情况已汇制成如图所示的两幅不完整的统计图,根据图中所经信息解答下列问题:
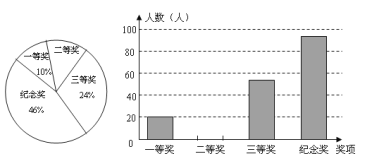
(1)这次知识竞赛共有多少名学生?
(2)浙江省委十三届四次全会提出,要以治污水、防洪水、排涝水、保供水、抓节水“五水共治”的重大决策, “二等奖”对应的扇形圆心角度数,并将条形统计图补充完整;
(3)小华参加了此次的知识竞赛,请你帮他求出获得“一等奖或二等奖”的概率。
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
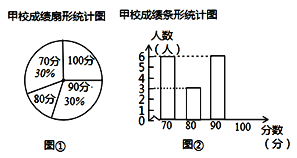
乙校成绩统计表
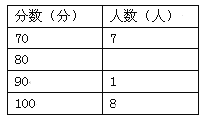
(1)在图①中,“80分”所在扇形的圆心角度数为 ;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;![]()
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
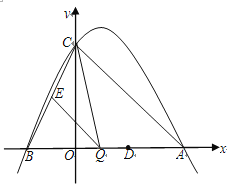
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ,当△CQE的面积为3时,求点Q的坐标;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与x轴交于点A(0,4)、E(0,-2)两点,与y轴交于点B(2,0),连结AB。过点A作直线AK⊥AB,动点P从点A出发以每秒![]() 个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处。
个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处。

(1)、求抛物线的解析式;
(2)、当点D在△ABP的内部时,△ABP与△ADP不重叠部分的面积为S,求S与t之间的函数关系式,并直接写出t的取值范围;
(3)、是否存在这样的时刻,使动点D到点O的距离最小,若存在请求出这个最小距离,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过十多年的成长,中国城市观众到影院观影的习惯已经逐渐养成:2010年,某影院观众人次总量才23400,但到2016年已经暴涨至13.5万.其中13.5万用科学计数法表示为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com