
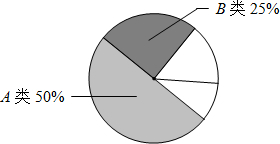
 期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:
期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:| 成绩(单位:分) | 频数 | 频率 |
| A类(80~100) | $\frac{1}{2}$ | |
| B类(60~79) | $\frac{1}{4}$ | |
| C类(40~59) | 8 | $\frac{1}{6}$ |
| D类(0~39) | 4 | $\frac{1}{12}$ |
| 学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
| 第一中学 | 71 | 52 | 432 | 0.75 |
| 第二中学 | 71 | 80 | 497 | 0.82 |
分析 (1)根据抽取得学生必须有代表性,能反映全年级学生的情况,可以采取随机抽样或随机分层抽样,据此即可得出正确答案;
(2)①利用抽取的学生数及C、D类的频数即可得出C、D类部分的频率,乘以360度可得答案;②用全年级总人数乘以样本中A、B类频率和即可得;
(3)此题答案不唯一,理由正确即可.
解答 解:(1)根据题意得:抽取得学生②和③更具有代表性,更能反映全年级学生的情况;
故答案为:②、③;
(2)①、C类部分的频率为$\frac{8}{48}$=$\frac{1}{6}$,圆心角度数为$\frac{8}{48}$×360°=60°,
D类部分的频率为$\frac{4}{48}$=$\frac{1}{12}$,圆心角度数为$\frac{4}{48}$×360°=30°,
②、估计全年级A、B类学生大约一共有12×48×($\frac{1}{2}$+$\frac{1}{4}$)=432(名),
故答案为:60°、30°、432,$\frac{1}{6}$、$\frac{1}{12}$;
(3)本题答案不唯一,以下两个答案仅供参考:
答案一:东海中学成绩较好,极差、方差小于南山中学,说明东海中学学生两极分化较小,学生之间的差距较南山中学小.
答案二:南山中学成绩较好,A、B类的频率和大于东海中学,说明南山中学学生及格率较东海中学学生好.
点评 此题考查了频数(率)分布表和扇形统计图的综合应用,解题的关键是根据统计图表所给的数据和频率=频数÷总数进行解答.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:填空题
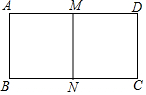 如图,矩形ABCD中,AB=4,M、N分别是AD、BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为4$\sqrt{2}$.
如图,矩形ABCD中,AB=4,M、N分别是AD、BC的中点,MN∥AB,若矩形DMNC与矩形ABCD相似,则AD的长为4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
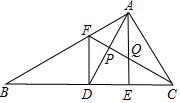 如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论
如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | tan52°-sin52° | B. | sin52°-tan52° | C. | 2-sin52°-tan52° | D. | -sin52°-tan52° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com