【题目】八（1）班组织了一次汉字听写比赛，甲、乙两队各10人，其比赛成绩如下表（10分制）：
甲队 | 7 | 8 | 9 | 10 | 10 | 10 | 10 | 9 | 9 | 8 |
乙队 | 7 | 7 | 8 | 9 | 10 | 10 | 9 | 10 | 10 | 10 |
（1）甲队成绩的中位数是 分，乙队成绩的众数是 分．
（2）计算甲队的平均成绩和方差_
（3）已知乙队成绩的方差是1.4，则成绩较为整齐的是 队．
【答案】9；10；1；甲
【解析】解：（1）把这组数据从小到大排列7，8，8，9，9，9，10，10，10，10，
甲队成绩的中位数是
=9；
∵在乙队中，10出现了5次，出现的次数最多，
∴乙队成绩的众数是10；
所以答案是：9，10；
（2）甲队的平均成绩是：
（7+8+9+10+10+10+10+9+9+8）=9，
方差是：[（7﹣9）2+2×（8﹣9）2+3×（9﹣9）2+4×（10﹣9）2]=1．
所以答案是：1
（3）∵乙队成绩的方差是1.4，甲队成绩的方差是1，
∴成绩较为整齐的是甲队．
所以答案是：甲．
【考点精析】关于本题考查的中位数、众数，需要了解中位数是唯一的，仅与数据的排列位置有关，它不能充分利用所有数据；众数可能一个，也可能多个，它一定是这组数据中的数才能得出正确答案．
科目：初中数学 来源： 题型：
【题目】若一个两位数的十位数字是a，个位数字是b，这个两位数恰好等于它的各位数字之和的4倍，则这样的两位数称为“巧数”．是巧数的两位数共有（ ）个．
A.l个
B.2个
C.3个
D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】两个全等的直角三角形ABC和DEF重叠在一起，其中∠A＝60°，AC＝4．固定△ABC不动，将△DEF进行如下操作：
(1)操作发现
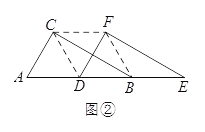
如图①，△DEF沿线段AB向右平移(即D点在线段AB内移动)，连接DC，CF，FB，四边形CDBF的形状在不断的变化，那么它的面积大小是否变化呢?如果不变化，请求出其面积．
(2)猜想论证
如图②，当D点移到AB的中点时，请你猜想四边形CDBF的形状，并说明理由．
(3)拓展探究
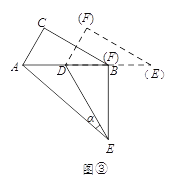
如图③，△DEF的D点固定在AB的中点，然后绕D点按顺时针方向旋转△DEF，使DF落在AB边上，此时F点恰好与B点重合，连接AE，求sin
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】人数相等的甲.乙两班学生参加了同一次数学测验，班平均分和方差分别为82分，82分，245分,190分那么成绩较为整齐的是（ ）
A. 甲班 B. 乙班 C. 两班一样整齐 D. 无法确定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在某中学举行的演讲比赛中，八年级5名参赛选手的成绩如下表所示
选手 | 1号 | 2号 | 3号 | 4号 | 5号 |
得分 | 92 | 95 | 91 | 89 | 88 |
（1）计算出这5名选手的平均成绩；
（2）计算出这5名选手成绩的方差．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某篮球队在一次联赛中共进行了10场比赛，已知10场比赛的平均得分为88分，且前9场比赛的得分依次为：97、91、85、91、84、86、85、82、88．
（1）求第10场比赛的得分；
（2）求这10场比赛得分的中位数，众数和方差．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB∥CD，分别探讨下面四个图形中∠APC与∠PAB，∠PCD之间的关系，请你从所得到的关系中任选一个加以证明。
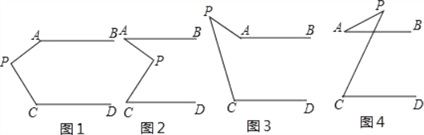
（1）在图1中，∠APC与∠PAB，∠PCD之间的关系是： ．
（2）在图2中，∠APC与∠PAB，∠PCD之间的关系是： ．
（3）在图3中，∠APC与∠PAB，∠PCD之间的关系是： ．
（4）在图4中，∠APC与∠PAB，∠PCD之间的关系是： ．
（5）在图 中，求证： ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com