
【题目】结合数轴与绝对值的知识解答下列问题:
(1) 数轴上表示3的点和2的点两点间的距离为________;
(2)如果在数轴上表示数a的点与表示 - 2的点的距离是3,那么a=________
(3)如果数轴上表示数a的点位于 -4与2之间,则![]() =_________
=_________
(4)a=_____时,![]() 有最小值,且最小值=________________
有最小值,且最小值=________________
(5)直接回答:当式子![]() 取最小值时,相应的a的取值范围是什么?
取最小值时,相应的a的取值范围是什么?
【答案】11或- 5; 61,9-1≤a≤5.
【解析】
(1)根据两点间的距离公式,可得答案;
(2)根据两点间的距离公式可得|a+2|=3,解方程可得答案;
(3)先计算绝对值,再合并同类项即可求解;
(4)根据线段上的点到线段两端点的距离的和最小,可得答案;
(5)根据线段上的点到线段两端点的距离的和最小,可得答案.
(1)数轴上表示3和2两点间的距离是32=1;
(2)依题意有
|a+2|=3,
解得a=5或1;
(3)∵数轴上表示数a的点位于4和2之间,
∴|a+4|+|a2|=a+4a+2=6;
(4)当a=1时,
|a+5|+|a1|+|a4|=6+0+3=9;
(5)|a+9|+|a+1|+|a5|+|a7|取最小值时,相应的a取值范围是![]() ,
,
最小值是a+9+a+1a+5a+7=22.


科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
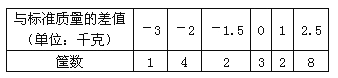
(1)20筐白菜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价26元,则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A.(﹣3,7)
B.(﹣1,7)
C.(﹣4,10)
D.(0,10)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有2个信封A、B,信封A装有四张卡片上分别写有1、2、3、4,信封B装有三张卡片分别写有5、6、7,每张卡片除了数字没有任何区别.从这两个信封中随机抽取两张卡片.
(1)请你用列表法或画树状图的方法描述所有可能的结果;
(2)把卡片上的两个数相加,求“得到的和是3的倍数”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
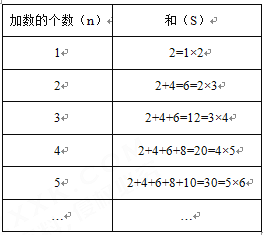
【题目】从2开始,连续的偶数相加,它的和的情况如下表:
(1)当n个最小的连续偶数相加时,它们的和s与n之间的关系式为s= (用含n的式子表示)
(2)并由此计算:
①2+4+6+8+…+50;
②52+54+56+…+100.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技开发公司研制出一种新型的产品,每件产品的成本为2400元,销售单价定为3000元,在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获得的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获得的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获得的利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时.求证:CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2![]() ,对角线AE,DF相交于点O,连接OC.求OC的长度.
,对角线AE,DF相交于点O,连接OC.求OC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列各题
![]() 比较大小:
比较大小:![]() ________
________![]() ;
;![]() ________
________![]() (用“
(用“![]() 、
、![]() 或
或![]() ”填空)
”填空)
![]() 画出数轴,在数轴上表示下列各数,并用“
画出数轴,在数轴上表示下列各数,并用“![]() ”连接:
”连接:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 将
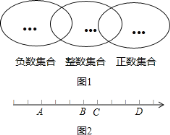
将![]() 有理数填入图
有理数填入图![]() 中它所属于的集合的圈内.
中它所属于的集合的圈内.
![]() 已知如图
已知如图![]() :数轴上
:数轴上![]() 、
、![]() 、
、![]() 、
、![]() 四点对应的有理数分别是整数
四点对应的有理数分别是整数![]() 、
、![]() 、
、![]() 、
、![]() ,且有
,且有![]() ,则原点应是________.
,则原点应是________.
![]() .
.![]() 点
点![]() .
.![]() 点
点![]() .
.![]() 点
点![]() .
.![]() 点.
点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com