
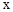 的方程
的方程
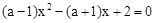 .
.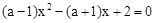 有两个不相等的实数根;
有两个不相等的实数根;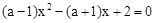 的根都是正整数.
的根都是正整数.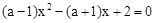 有两个不相等的实数根,则△>0,且二次项系数不为0,列出不等式组,即可求出a的取值范围.
有两个不相等的实数根,则△>0,且二次项系数不为0,列出不等式组,即可求出a的取值范围.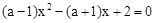 都是正整数根,得出a的取值范围,即可得出答案.
都是正整数根,得出a的取值范围,即可得出答案.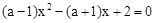 有两个不相等的实数根,
有两个不相等的实数根,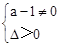 ,即
,即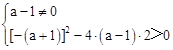 ,即
,即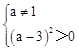 ,即
,即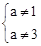 .
.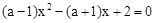 有两个不相等的实数根.
有两个不相等的实数根.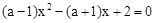 .
.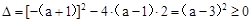 .
. ,解得x1=1,
,解得x1=1,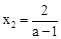 .
.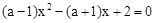 都是正整数根,∴只需
都是正整数根,∴只需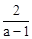 为正整数.
为正整数.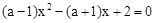 的根都是正整数.
的根都是正整数.

科目:初中数学 来源:不详 题型:解答题
| | 每天的销售量/台 | 每台销售利润/元 |
| 降价前 | 8 | 400 |
| 降价后 | | |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 没有实数根,即不存在一个实数的平方等于
没有实数根,即不存在一个实数的平方等于 .若我们规定一个新数“
.若我们规定一个新数“ ”,使其满足
”,使其满足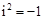 (即方程
(即方程 有一个根为
有一个根为 ).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有
).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有 ,从而对于任意正整数
,从而对于任意正整数 ,我们可以得到
,我们可以得到 ,同理可得
,同理可得 ,
, ,
, .那么
.那么 的值为 .
的值为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.289(1―2x)=256 | B.256(1+x)2=289 |
| C.289(1―x)2=256 | D.289―289(1―x)―289(1―x)2=256 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com