
| A. | 正方形 | B. | 正六边形 | C. | 正八边形 | D. | 正十二边形 |
分析 由镶嵌的条件知,在一个顶点处各个内角和为360°.依此即可解答.
解答 解:A、正三角形的每个内角是60°,正方形的每个内角是90°.∵3×60°+2×90°=360°,∴正方形能匹配;
B、正六边形的每个内角是120°,正三角形的每个内角是60度.∵2×120°+2×60°=360°,或120°+4×60°=360°,∴正六边形能匹配;
C、正三角形的每个内角是60°,正八边形内角为135°,显然不能构成360°的周角,故不能匹配.
D、正三角形的每个内角是60°,正十二边形的每个内角是180°-360°÷12=150°,∵60°+2×150°=360°,∴正十二边形能匹配;
故选C.
点评 考查了平面镶嵌(密铺).几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
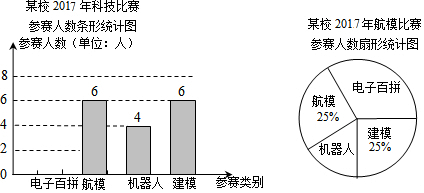
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
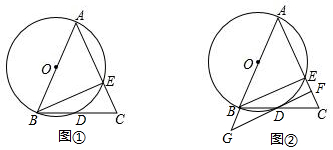
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (m-8%)(m+9%)万元 | B. | (1-8%)(1+9%)m万元 | C. | (m-8%+9%)万元 | D. | (m-8%+9%)m万元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
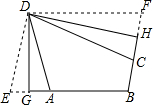 定义:有三个内角相等凸四边形叫三等角四边形.
定义:有三个内角相等凸四边形叫三等角四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
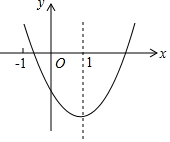 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:| A. | ①④ | B. | ②④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com