
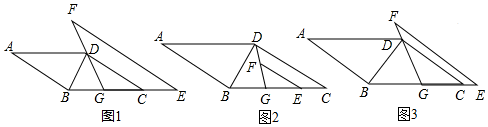
分析 (1)先根据直角三角形斜边上中线的性质,求得BC的长,再根据勾股定理,求得CD的长,最后根据三角形中位线定理,求得EF的长即可;
(2)先延长DG交AB的延长线于H点,根据GD平分∠BDC,得到△BDH是等腰直角三角形,得出DH=$\sqrt{2}$DB,然后判定△BGH≌△EGF(AAS),得到GH=FG,最后根据DH=FH+DF,即可得到$\sqrt{2}$DB=2FG+DF;
(3)先延长DG交AB的延长线于H点,根据∠GDC=∠H=30°,得出DH=2DB,然后判定△BGH≌△EGF(AAS),得到GH=FG,最根据DH=FH-DF,即可得到2DB=2FG-DF.
解答  解:(1)如图1,在平行四边形ABCD中,AB∥CD,
解:(1)如图1,在平行四边形ABCD中,AB∥CD,
∴∠BDC=∠ABD=90°,
∵在Rt△BDC中,G为BC的中点,DG=$\sqrt{5}$,
∴BC=2DG=2$\sqrt{5}$,
又∵tanA=tan∠BCD=$\frac{1}{2}$,
∴CD=2BD,
故可设BD=x,CD=2x,则
Rt△BCD中,x2+(2x)2=(2$\sqrt{5}$)2,
解得x=2,
∴CD=4,
又∵CE=CG,CD∥EF,
∴D为GF的中点,
∴EF=2CD=8;
(2)如图2,延长DG交AB的延长线于H点,则∠DBH=90°,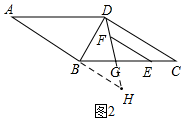
∵AB∥CD,
∴∠BDC=∠ABD=90°,
又∵GD平分∠BDC,
∴∠BDH=∠CDH=45°,
∴△BDH是等腰直角三角形,
∴DH=$\sqrt{2}$DB,
又∵EF∥CD,
∴EF∥AB,
∴∠F=∠H,∠E=∠HBG,
又∵G为BE的中点,
∴BG=EG,
∴△BGH≌△EGF(AAS),
∴GH=FG,
∵DH=FH+DF,
∴$\sqrt{2}$DB=2FG+DF;
(3)若E点在BC延长线上,G为BE中点,且∠GDC=30°,则(2)中的结论不成立,正确结论为:2DB=2FG-FD.
证明:如图3,延长DG交AB的延长线于H点,则∠DBH=90°,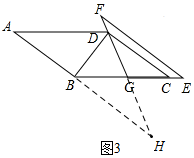
∵AB∥CD,
∴∠GDC=∠H=30°,
∴DH=2DB,
又∵EF∥CD,
∴EF∥AB,
∴∠F=∠H,∠E=∠HBG,
又∵G为BE的中点,
∴BG=EG,
∴△BGH≌△EGF(AAS),
∴GH=FG,
∵DH=FH-DF,
∴2DB=2FG-DF.
点评 本题主要考查了全等三角形的判定与性质、直角三角形斜边上的中线的性质、等腰直角三角形的性质、含30°角的直角三角形的性质以及勾股定理的综合应用,解决问题的关键是作辅助线构造全等三角形,根据全等三角形的对应边相等进行求解.解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半;在直角三角形中,斜边上的中线等于斜边的一半.


科目:初中数学 来源: 题型:解答题
 已知:等边△OAB的边长为3,另一等腰△OCA与△OAB有公共边OA,且OC=AC,∠C=120°.现有两动点P、Q分别从B、O两点同时出发,点P以每秒3个单位的速度沿BO向点O运动,点Q以每秒1个单位的速度沿OC向点C运动,当其中一个点到达终点时,另一个点也随即停止运动.请回答下列问题:
已知:等边△OAB的边长为3,另一等腰△OCA与△OAB有公共边OA,且OC=AC,∠C=120°.现有两动点P、Q分别从B、O两点同时出发,点P以每秒3个单位的速度沿BO向点O运动,点Q以每秒1个单位的速度沿OC向点C运动,当其中一个点到达终点时,另一个点也随即停止运动.请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
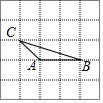 如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
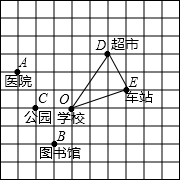 如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题:
如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com