【题目】如图，面积为8的矩形ABOC的边OB、OC分别在x轴、y轴的正半轴上，点A在双曲线y＝
的图象上，且AC＝2．
（1）求k值；
（2）矩形BDEF，BD在x轴的正半轴上，F在AB上，且BD＝OC，BF＝OB．双曲线交DE于M点，交EF于N点，求△MEN的面积．
【答案】(1)y＝
；(2) 
【解析】试题分析：（1）根据矩形的面积求出AB，求出A的坐标，代入反比例函数解析式求出即可；
（2）先求出BF和OD，代入函数解析式求出点的坐标，求出EN和EM，根据面积公式求出即可．
试题解析：解：（1）∵矩形ABOC的面积为8，AC=2，∴OC=AB=8÷2=4，AC=OB=2，∴A点的坐标为（2，4），∵点A在双曲线
的图象上，∴代入得：k=8；
（2）由（1）知：反比例函数的解析式为
，∵BD=OC，BF=OB，OC=4，OB=2，又∵四边形BDEF是矩形，∴BD=EF=4，BF=DE=2，OD=BD+OB=6，把y=2代入
得：x=4，即N点的坐标为（4，2），把x=6代入
得：y=
，即M的坐标为（6， 
），∴EN=6﹣4=2，EM=2﹣
=
，∴△MEN的面积为
=
．
科目：初中数学 来源： 题型：
【题目】阅读与思考：整式乘法与因式分解是方向相反的变形
由（x+p）(x+q)=x2+(p+q)x+pq得x2+(p+q)x+pq=（x+p）(x+q)
利用这个式子可以将某些二次项系数是1的二次三项式分解因式,
例如：将式子x2+3x+2分解因式.
分析：这个式子的常数项2=1×2一次项系数3=1+2
所以x2+3x+2=x2+(1+2)x=1×2
解：x2+3x+2=(x+)(x+2)
请仿照上面的方法,解答下列问题：
(1)分解因式：x2+6x-27＝__________________；
(2)若x2+px+8可分解为两个一次因式的积,则整数
的所有可能值是_________________;
(3)利用因式分解法解方程：x2-4x-12=0..
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线
分别与
轴、
轴交于点
、
，且与直线
交于点
．
（1）若
是线段
上的点，且
的面积为
，求直线
的函数表达式．
（
）在（
）的条件下，设
是射线上的点，在平面内是否存在点
，使以
、、、为顶点的四边形是菱形？若存在，直接写出点的坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】程大位所著《算法统宗》是一部中国传统数学重要的著作．在《算法统宗》中记载：“平地秋千未起，踏板离地一尺．送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索长有几？”【注释】1步=5尺．
译文：“当秋千静止时，秋千上的踏板离地有1尺高，如将秋千的踏板往前推动两步（10尺）时，踏板就和人一样高，已知这个人身高是5尺．美丽的姑娘和才子们，每天都来争荡秋千，欢声笑语终日不断．好奇的能工巧匠，能算出这秋千的绳索长是多少吗？”
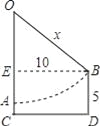
如图，假设秋千的绳索长始终保持直线状态，OA是秋千的静止状态，A是踏板，CD是地面，点B是推动两步后踏板的位置，弧AB是踏板移动的轨迹．已知AC=1尺，CD=EB=10尺，人的身高BD=5尺．设绳索长OA=OB=x尺，则可列方程为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个，小明做摸球试验，他将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是试验中的一组统计数据：
(1)请估计：当n很大时，摸到白球的概率约为______；(精确到0.1)
(2)估算盒子里有白球________个；
(3)若向盒子里再放入x个除颜色以外其他完全相同的球，这x个球中白球只有1个，每次将球搅拌均匀后，任意摸出一个球记下颜色再放回，通过大量重复摸球试验后发现，摸到白球的频率稳定在50%，请推测x的值最有可能是多少．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知，在△ABC中，∠B＜∠C，AD平分∠BAC，E的线段AD(除去端点A、D)上一动点，EF⊥BC于点F.
(1)若∠B＝40°，∠DEF＝10°，求∠C的度数．
(2)当E在AD上移动时，∠B、∠C、∠DEF之间存在怎样的等量关系？请写出这个等量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知正比例函数y1＝－
x与反比例函数y2＝
的图象经过A（－2，1）点，求：
（1）反比例函数的解析式．
（2）正比例与反比例函数另一个交点B的坐标．
（3）当x在什么范围，y1＝y2，当x在什么范围，y1＜y2，当x在什么范围，y1＞y2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】实验与探究：
（
）由图观察易知
关于直线
的对称点
的坐标为
，请在图中分别标明
、
关于直线
的对称点
、
的位置，并写出他们的坐标：__________、__________．
归纳与发现：
（
）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点
关于第一、三象限的角平分线的对称点
的坐标为__________（不必证明）．
运用与拓广：
（
）已知两点
、
，试在直线上确定一点
，使点到
、
两点的距离之和最小，并求出点坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，把△ABC纸片沿DE折叠，当点A在四边形BCDE的外部时，记∠AEB为∠1，∠ADC为∠2，则∠A、∠1与∠2的数量关系，结论正确的是（ ）
A. ∠1＝∠2＋∠A B. ∠1＝2∠A＋∠2
C. ∠1＝2∠2＋2∠A D. 2∠1＝∠2＋∠A
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com